キーワード
おさらい
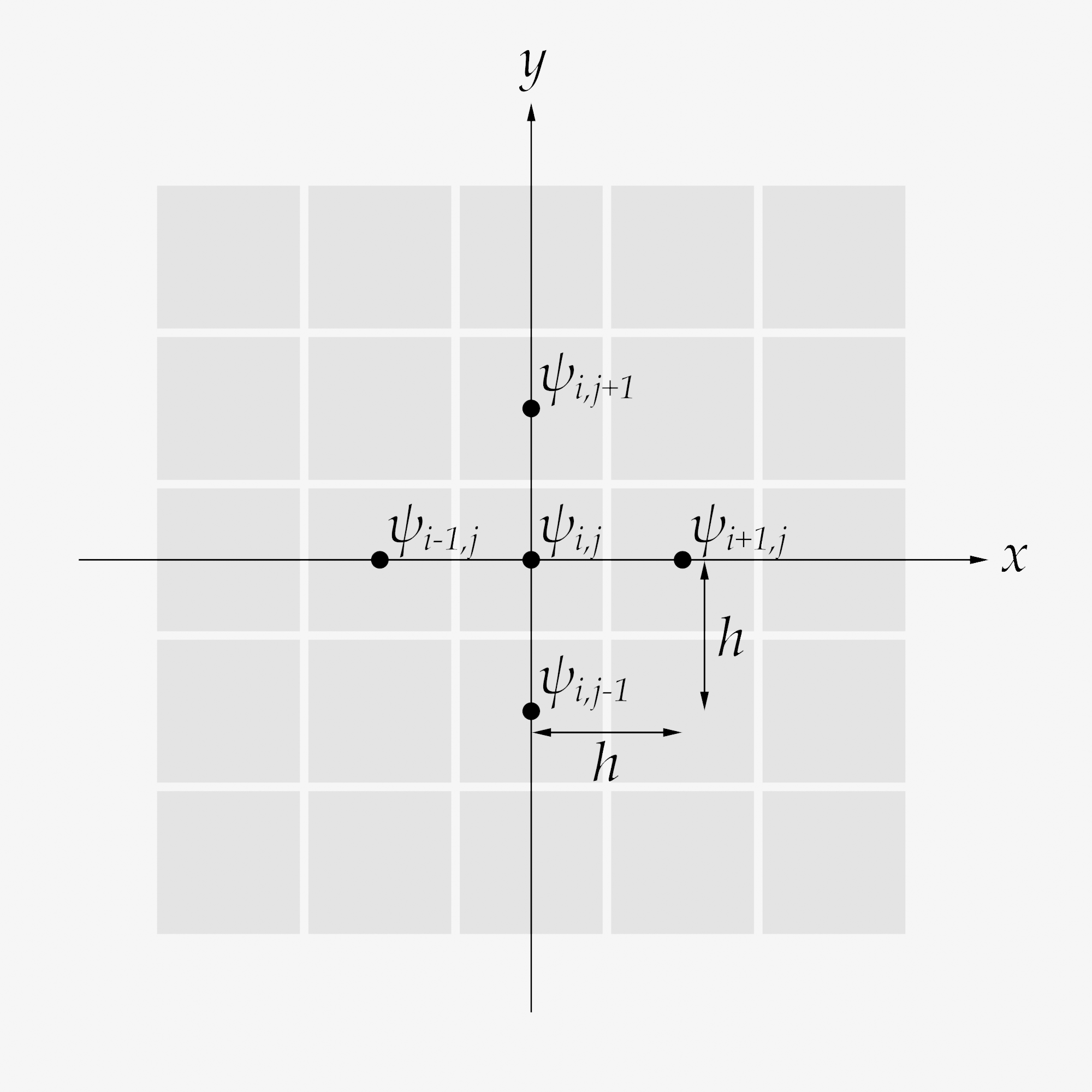
『偏微分方程式の数値計算入門(1/3)』の続きです.テイラー展開とか使うと格子座標\( i,j \)についての微分係数を簡単な多項式に置き換えることができた.
1階偏微分
\[ \small{ \frac{\partial \psi(x_{i,j}, y_{i,j})}{\partial x} \approx \frac{\psi_{i+1, j} - \psi_{i, j}}{h}, \ \frac{\partial \psi(x_{i,j}, y_{i,j})}{\partial y} \approx \frac{\psi_{i, j+1} - \psi_{i, j}}{h} (前進差分近似)} \]
\[ \small{ \frac{\partial \psi(x_{i,j}, y_{i,j})}{\partial x} \approx \frac{\psi_{i, j} - \psi_{i-1, j}}{h}, \ \frac{\partial \psi(x_{i,j}, y_{i,j})}{\partial y} \approx \frac{\psi_{i, j} - \psi_{i, j-1}}{h} (後進差分近似)} \]
\[ \small{ \frac{\partial \psi(x_{i,j}, y_{i,j})}{\partial x} \approx \frac{\psi_{i+1, j} - \psi_{i-1, j}}{2h}, \ \frac{\partial \psi(x_{i,j}, y_{i,j})}{\partial y} \approx \frac{\psi_{i, j+1} - \psi_{i, j-1}}{2h} (中心差分近似)} \]
2階偏微分
\[
\small{
\frac{\partial^2 \psi(x_{i,j}, y_{i,j})}{\partial x^2} \approx \frac{\psi_{i+1, j} - 2\psi_{i, j} + \psi_{i-1, j}}{h^2}, \frac{\partial^2 \psi(x_{i,j}, y_{i,j})}{\partial y^2} \approx \frac{\psi_{i, j+1} - 2\psi_{i, j} + \psi_{i, j-1}}{h^2}
}
\]
定常な場合の方程式を考える
ここからは実際の方程式について考えていきます."定常"というのは「時間的に変化しない」という意味です.つまり,式に中に変数\( t \)が含まれないものになります.まずは超シンプルな例を見てみましょう.\[
\nabla^2 \psi = 0
\]
とてもシンプルな式ですよね.上式はラプラス方程式と呼ばれているもので,時間的に変化の無い場合(定常状態)における熱伝導の様子を表しているんだそうだ.この式が様々な方程式の基本形になっているパターンが多いです. 右辺が変わったり,項が追加されたり,これだけでも色々バリエーションが考えられます.
今回は2次元を考えていきたいので,以下のように\( \nabla^2 \)(ラプラシアン)を展開していきます.
\[
\frac{\partial^2 \psi}{\partial x^2} + \frac{\partial^2 \psi}{\partial y^2} = 0
\]
\( \psi \)は未知の関数(場)と考えてください.すなわち\( \psi \)は2変数(\( x, y \))の関数となります.
\[
\psi = \psi(x, y)
\]
式中の2階偏微分を\(i, j\)地点の微分係数とみなして差分近似していきます.偏微分記号を多項式に置き換えただけです.
\[
\frac{\psi_{i+1, j} - 2\psi_{i, j} + \psi_{i-1, j}}{h^2} + \frac{\psi_{i, j+1} - 2\psi_{i, j} + \psi_{i, j-1}}{h^2} = 0
\]
\( \psi_{i, j} \)について解くと,
\[
\psi_{i, j} = \frac{1}{4} (\psi_{i+1, j} + \psi_{i-1, j} + \psi_{i, j+1} + \psi_{i, j-1})
\]
\( \psi_{i, j} \)は近傍の状態で決定されるという式になります.この計算を全ての点において何度も繰り返していくと,初期状態に関わらず(境界条件のみによって決定される)一定の状態に\( \psi \)の値が収束していきます.
そこでこんな漸化式を考えてみましょう.この反復法はヤコビ法と呼ばれます.
ヤコビ法
\[
\psi_{i, j}^{(n+1)} = \frac{1}{4} (\psi_{i+1, j}^{(n)} + \psi_{i-1, j}^{(n)} + \psi_{i, j+1}^{(n)} + \psi_{i, j-1}^{(n)})
\]
何回目の計算かを示す文字を\( n \)として,\( \psi \)の右上に添え字として表記しています.右上に\( n \)とついているものは「既知の古い値」,\( n+1 \)とついているものは「計算によって更新された新しい値」ということになります.
ここで少しプログラミングによる計算方法を考えてみましょう.この漸化式を計算するには「古い値」を格納する配列と,「新しい値」を格納する配列の2つが必要になってきます.
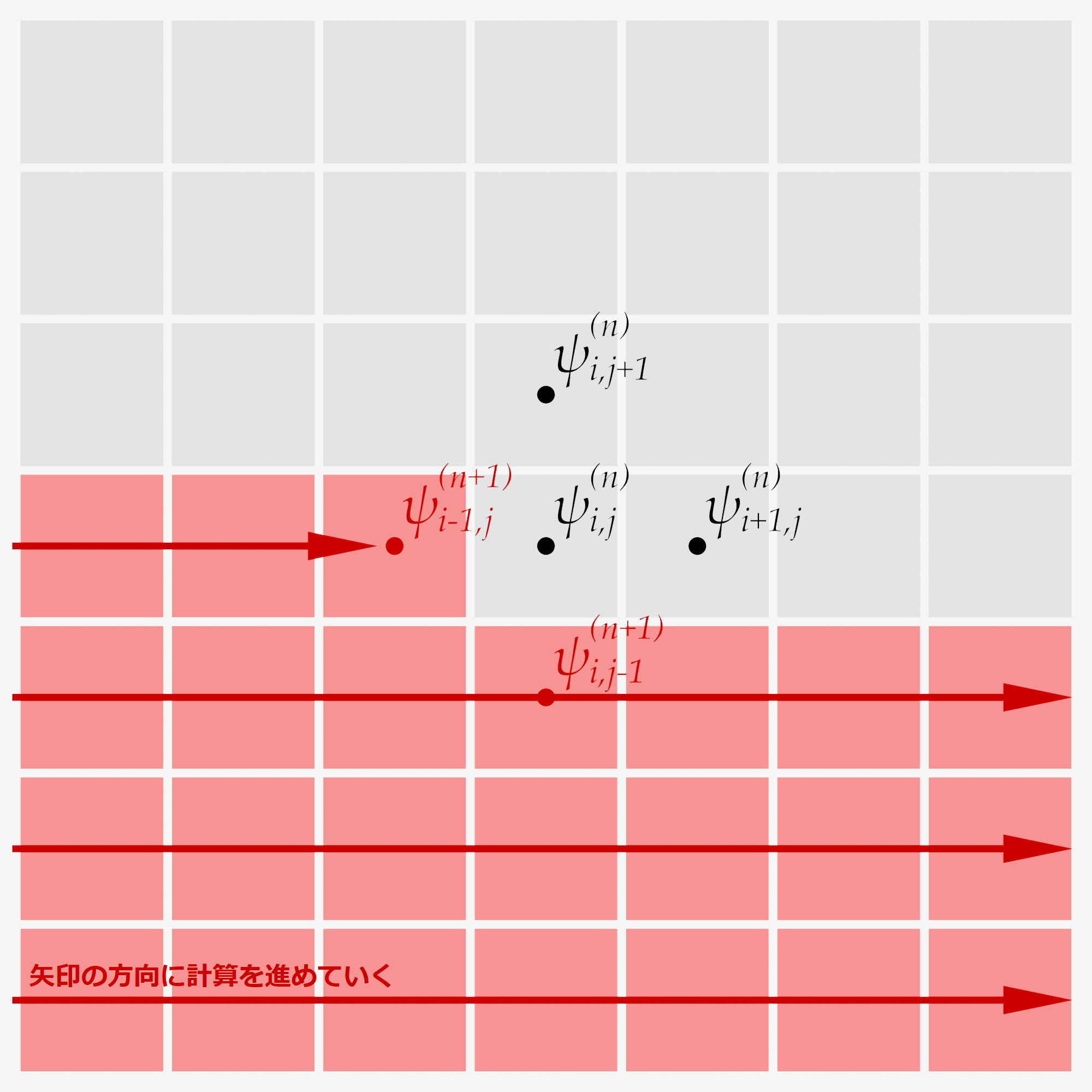
もちろん丁寧に配列を2つ用意して計算してもいいのですが,配列を2つ用意して管理するのって面倒ですよね(本音).この計算を何とか1つの配列でできないものでしょうか.これを解決するのが"ガウス=ザイデル法"という反復法になります.
まあ,別に大した話ではなく,実際にプログラミングをしている人なら誰でも思いつくような方法です.ガウス=ザイデル法ではこんな漸化式を考えます.
ガウス=ザイデル法
\[
\psi_{i, j}^{(n+1)} = \frac{1}{4} (\psi_{i+1, j}^{(n)} + \psi_{i-1, j}^{(n+1)} + \psi_{i, j+1}^{(n)} + \psi_{i, j-1}^{(n+1)})
\]
右辺に「古い値」と,「新しい値」が混じっている状態です.これは図で見て頂くのが一番わかりやすいと思います.\( \psi \)の情報を格納する配列を1つだけ用意して,値を順次更新しながら計算を進めていくというだけのことです.
この計算方法を見てわかる通り,全ての場合についてガウス=ザイデル法を採用することがベストだとは言い切れないことがわかると思います. 今回はじわじわと収束していくような場合を考えているのでガウス=ザイデル法を採用しても問題はないですが,当然この計算方法が適さない場合もあります. どの計算方法を採用するかどうかについては注意が必要なところです.
実際に計算してみる
偏微分方程式を解くには初期条件と境界条件が必要になります.ただし,今回は定常な場合を考えているので初期条件を気にする必要はありません.計算条件を以下のように定義します.
\[
\frac{\partial^2 \psi}{\partial x^2} + \frac{\partial^2 \psi}{\partial y^2} = 0 ; 0 \leq x \leq 1, 0 \leq y \leq 1
\]
境界条件は以下のように定義します.
\[
\psi(0, y) = 0 \\
\psi(1, y) = 0 \\
\psi(x, 0) = 0 \\
\psi(x, 1) = 4x(1-x)
\]
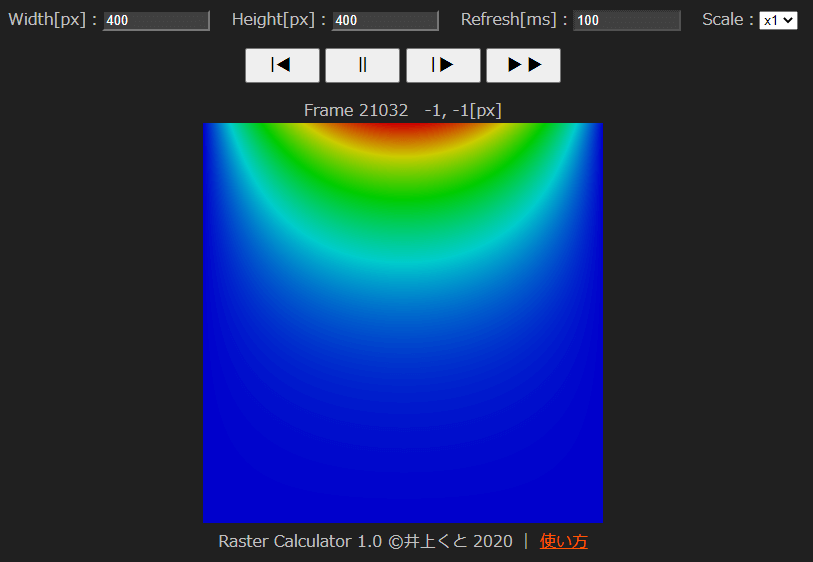
こちらに計算プログラムを用意してみました.(ブラウザで動きます)
計算結果です.実際に動かすとよくわかると思うのですが,じわ~っと広がっていく様子が観測できます.なるほど,確かに熱伝導っぽい.そして収束がめちゃくちゃ遅い.
どんどん収束していくのですが,どこで計算を打ち切ればよいのかという疑問が当然沸いてくると思います.1つの目安になる判断方法として,「相対誤差が一定値より下回った時に計算を打ち切る」という方法があります.
各格子の点に対して相対誤差を定義して,指定したある一定の閾値\( \varepsilon \)より小さくなるまで計算するという条件を与えるだけです.
\[
\left| \frac{\psi_{i,j}^{(n+1)} - \psi_{i,j}^{(n)}}{\psi_{i,j}^{(n+1)}} \right| \leq \varepsilon
\]
ただし,毎回これを全格子に対して計算して条件分岐させると無駄に計算量が増えて非効率なので,以下のように全格子について相対誤差の合計を先に算出してから,最後に1回だけ(1フレームにつき)条件分岐させるのが良いでしょう.
\[
\frac{ \displaystyle \sum_i \displaystyle \sum_j | \psi_{i,j}^{(n+1)} - \psi_{i,j}^{(n)} | }{ \displaystyle \sum_i \displaystyle \sum_j | \psi_{i,j}^{(n+1)}| } \leq \varepsilon
\]
SOR法
計算はできるのはわかったけど,収束が遅くてなかなか計算打切りまでたどり着けない! そんなあなたに,収束を加速させる方法があるんです.知りたいですよねえ.今回のようにめちゃくちゃ収束が遅いときに,収束を加速させることができるSOR法というものがあります. 考え方は決して難しいものではありません.「1フレーム毎の補正量が小さいなら,補正量になんか1より大きい係数掛けてやれば収束が加速するんじゃね」っていう発想です.
ここでガウス=ザイデル法による漸化式を思い出してください.ここから少しだけ式を変形します.
ガウス=ザイデル法
\[
\psi_{i, j}^{(n+1)} = \frac{1}{4} (\psi_{i+1, j}^{(n)} + \psi_{i-1, j}^{(n+1)} + \psi_{i, j+1}^{(n)} + \psi_{i, j-1}^{(n+1)})
\]
右辺に\( \psi_{i,j}^{(n)} - \psi_{i,j}^{(n)} \)を加えてみます.プラマイ0なので値は変わりません.
\[
\psi_{i, j}^{(n+1)} = \psi_{i,j}^{(n)} + \left\{ \frac{1}{4} (\psi_{i+1, j}^{(n)} + \psi_{i-1, j}^{(n+1)} + \psi_{i, j+1}^{(n)} + \psi_{i, j-1}^{(n+1)}) - \psi_{i,j}^{(n)} \right\}
\]
何をしたのか,おわかりいただけただろうか.式の形をよく見て見ると\( \psi_{i, j}^{(n+1)} = \psi_{i,j}^{(n)} + [補正量] \) という形になっていることがわかると思います.
この補正量に1より大きい係数\( \omega \)を掛けると収束が加速しそうな気がします.つまり,以下のような漸化式を考えれば収束が加速することがわかります.
\[
\psi_{i, j}^{(n+1)} = \psi_{i,j}^{(n)} + \omega \left\{ \frac{1}{4} (\psi_{i+1, j}^{(n)} + \psi_{i-1, j}^{(n+1)} + \psi_{i, j+1}^{(n)} + \psi_{i, j-1}^{(n+1)}) - \psi_{i,j}^{(n)} \right\}
\]
理屈はわかったけど「\( \omega \)って具体的になんぼだよ」と思った方,大丈夫です.ちゃんと\( \omega \)を決定する計算式があります.
適切な\( \omega \)の値は格子数によって決まります.格子数\(m \times n\)のとき,\( \omega \)の値は下式で与えられます.
\[
\omega = \frac{2}{1 + \sqrt{1 - (\mu / 2)^2}} \\
\mu = \cos \frac{\pi}{m} + \cos \frac{\pi}{n}
\]
このように決定された\( \omega \)を補正量に掛けて計算すると非常に効率よく計算ができます.
次回は"非定常な場合"の方程式を考えていきます.方程式に\( t \)が登場しますよ.
偏微分方程式の数値計算入門(3/3)