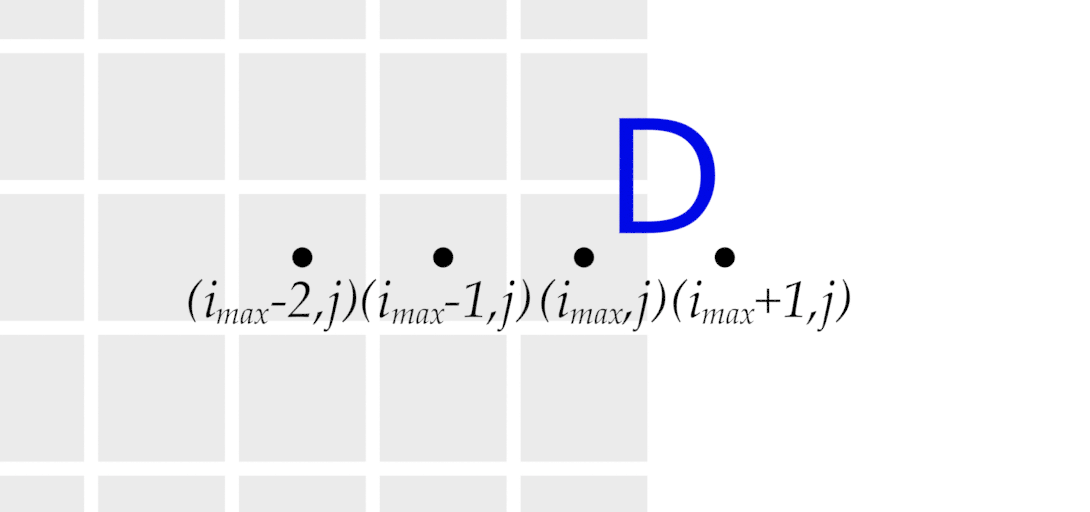キーワード
はじめに
今回はナビエ・ストークス方程式を用いた流体シミュレーションの実装に向けたアルゴリズム解説を行います. 厳密な話は抜きにして,ざっくりな計算の流れと「この式を使えばとりあえず実装できるんだ」っていう部分を重点的に解説していきたいと思います.
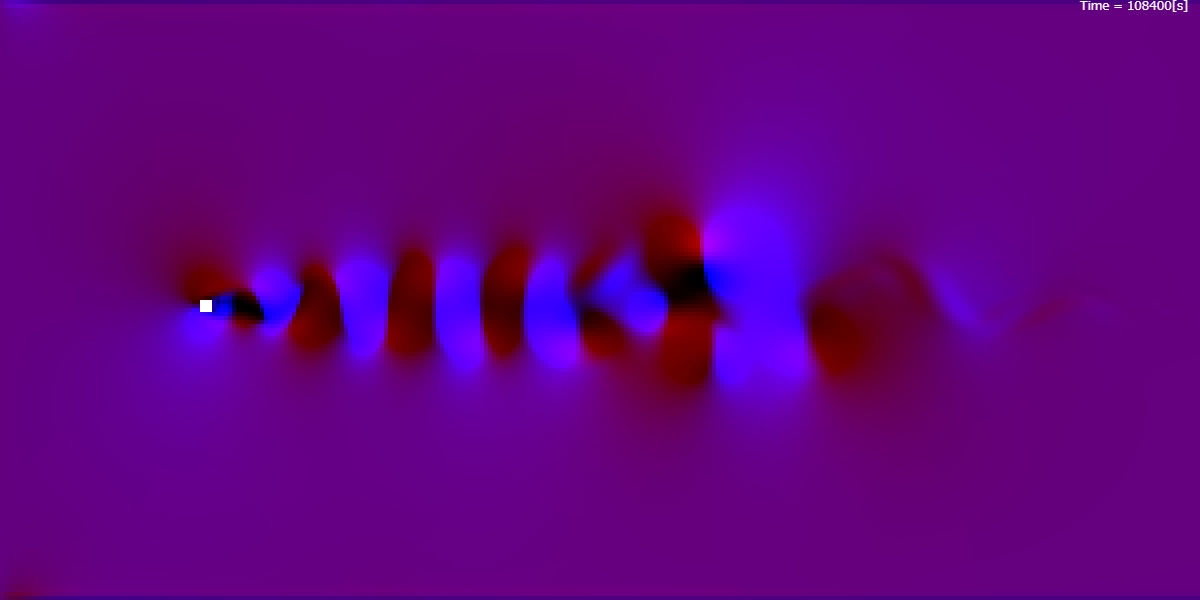
こんなのが作れるようになることを目標とします.
というわけで今回はパっと見エグい数式が沢山登場しますが,決して難解な内容ではない(理解している人は皆そう言う)のでどうか最後までお付き合いして頂けると幸いです.
とはいえ,ある程度は前提知識が必要にはなってくるので以下の人を対象としたいと思います.
- 基本的なベクトル演算の方法を知っている
- ベクトルとスカラーの区別がしっかりできる
- 微分・偏微分の基本的な原理を理解している
- ∇(ナブラ)記号を見てもビビらない
ナビエ・ストークス方程式をざっくり理解してみる
流体シミュレーションについて色々調べてみると,どうやらナビエ・ストークス方程式というのを使うらしい. 条件によっていくつか種類があるみたいだが,ウィキペディアによると一般的にはこんな式がよく使われるのだそうだ.\[
\frac{\partial \vec{v}}{\partial t} + (\vec{v} \cdot \nabla) \vec{v} = - \frac{1}{\rho} \nabla p + \nu \nabla^2 \vec{v} + \vec{g}
\]
そしてもう一つ,おまけみたいについている下の式.どうやらこれも条件として加えないと解が定まらないらしい.
\[
\nabla \cdot \vec{v} = 0
\]
しかし,2つ目の式は数値計算をするときに直接使うものではなく,この式を元に別の数値計算用の式を導出するときに使うんだそうです. それよりも注目すべきは,流速\( \vec{v} \)と圧力\( p \)です.その他の文字は流体の性質を決める定数です.つまり流体とは流速と圧力の状態によって動きが決定されるということがこの式からわかります.
ここで,偏微分方程式について少し解説をします.この手の計算では場という概念が必要になってきます.つまり特定の一点の話ではなく,ある程度広がりを持った空間を考える必要があります. 思い出してみてください,普通の方程式は解として特定の数値が求まりますが,微分方程式は解として関数が求まります.
つまり,今見ている\( \vec{v} \)や\( p \)というのは未知関数という扱いになります.上式では完全に省略されていますが,敢えて表記するなら以下のようになります.
\[
\vec{v} ⇒ \vec{v} (x, y, t) \\
p ⇒ p (x, y, t)
\]
これが意味するのは関数に入力される座標\( (x, y) \)によって,出力される値が変わるということです.直感的に理解できるようなイメージとしては,空間にその場所の流速や圧力の大きさを示した数字がびっしり並んでいるような状態です. このように空間座標を変数とした関数で状態を定義する考え方を場と呼んでいます. まずはこの考え方に慣れてください.
ここから先は,よりボヤっとした話をしていきます.全てを理解する必要はないですが,知っておくとプログラミング時に間違いに気づきやすくなるかもしれません.
結局のところ,ナビエ・ストークス方程式は何を表しているのでしょうか.そもそも偏微分方程式を見ただけで動きが想像できる人なんているのか(困惑)って感じですよねえ.
まあ細かい話は抜きにして,まずは全体のイメージからですが,ナビエ・ストークス方程式を見ると何やら足し算でたくさん繋がってますねえ.それぞれの項には意味があり,名前も付いています. 簡単に言ってしまえば,この足し算は複数の力が合わさっていることを意味しています.
では,それぞれの項はどんな意味を持つのか,これについてもざっくりな説明しかできませんが大体以下の通りです.
\( \frac{\partial \vec{v}}{\partial t} + (\vec{v} \cdot \nabla) \vec{v} \) …
2つ合わせて加速度項なんて呼ばれています.意味としては\( ma = F \)の中の\( a \)みたいなものです.
\( - \frac{1}{\rho} \nabla p \) …
圧力の高い部分から低い部分に流れるといった動きを表しています.面白いのは全体の圧力の大小に関わらず,近傍との圧力の差のみが効いてくるということですね.
\( \nu \nabla^2 \vec{v} \) …
流体の粘性に関する性質を表しています.ラプラシアンは直感的に理解するのが少し難しいのですが,変形のしづらさを表しています. この項の値が大きければ滑らかな流れになり, 逆に小さくなるとウネウネと渦を作るような流れになります.
\( \vec{g} \) …
重力など,全体に均一に働く外力です.
∇を展開してみる
\( \nabla \)そのものは決して難しいものではありません.記号の後ろにつく文字を各成分方向に偏微分するだけです.\[
\nabla = ( \frac{\partial}{\partial x}, \frac{\partial}{\partial y})
\]
そうです,これだけなんです.ベクトルの計算ができれば何も躓くことなんかないんです.
なんだ楽勝じゃないか(そう思ってた時期が私にもありました).
――意外と躓きました orz
わかってる方は読み飛ばして問題無いですが,自分が躓いた点について少し説明していきたいと思います.
まずはこいつ → \( \nabla^2 \)(ラプラシアン)についてです.先ほどの\( \nabla \)について,\( \nabla \)同士で内積をとったものをラプラシアンとしています.式で書くと以下の通りです.
\[
\nabla^2 = \nabla \cdot \nabla = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}
\]
\( \nabla \)はベクトルとして扱えます.内積をとっているのだから結果は当然スカラーになるのですが,なぜか私はここで躓きました.\( \nabla^2 \)がただの記号ということにもう少し早く気づければよかったのですが, 最初にこの記号を見たとき私は\( \nabla \)を2乗してるんだなとか,2階微分だから添え字として2をつけてるんだなとか,それじゃあ\( \nabla^3 \)のときはどうなるんだろうかとか訳のわからないことを考えてましたよ.
まあ結論として,\( \nabla^2 \)は記号として誤解を招きやすいので注意が必要ということですね.何度でも言いますが,\( \nabla^2 \)はただの記号です.間違っても\( \nabla \)の2乗とか言っちゃいけないです.
それともう一つ,\( \nabla^2 \)の後ろにつく関数はスカラーとベクトルの両方をとり得るということですね.これも誰かがそう決めたただのルールなので素直に受け入れましょう.式で書くならこんな感じ.
\[
\nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} \\
\nabla^2 \vec{g} = \frac{\partial^2 \vec{g}}{\partial x^2} + \frac{\partial^2 \vec{g}}{\partial y^2} = (\frac{\partial^2 g_x}{\partial x^2} + \frac{\partial^2 g_x}{\partial y^2}, \frac{\partial^2 g_y}{\partial x^2} + \frac{\partial^2 g_y}{\partial y^2})
\]
ここまで来たらもう展開できそうですが,最後にもう一つ注意点を.これも当たり前の話ですが,括弧が無ければ必ず左から右に計算してくださいね.ベクトルの計算なので項の中で勝手に計算の順番を入れ替えるのはダメです.
以上を踏まえて,展開したナビエ・ストークス方程式がこちらになります.
\[
\frac{\partial \vec{v}}{\partial t} + v_x \frac{\partial \vec{v}}{\partial x} + v_y \frac{\partial \vec{v}}{\partial y}
= - \frac{1}{\rho} (\frac{\partial p}{\partial x}, \frac{\partial p}{\partial y}) + \nu(\frac{\partial^2 \vec{v}}{\partial x^2} + \frac{\partial^2 \vec{v}}{\partial y^2}) + \vec{g}
\]
さらに,\( x \)成分と\( y \)成分を分けると以下のようになります.
\[
\left
\{ \begin{eqnarray}
&\frac{\partial v_x}{\partial t} + v_x \frac{\partial v_x}{\partial x} + v_y \frac{\partial v_x}{\partial y}
= - \frac{1}{\rho} \frac{\partial p}{\partial x} + \nu(\frac{\partial^2 v_x}{\partial x^2} + \frac{\partial^2 v_x}{\partial y^2}) + g_x \\
&\frac{\partial v_y}{\partial t} + v_x \frac{\partial v_y}{\partial x} + v_y \frac{\partial v_y}{\partial y}
= - \frac{1}{\rho} \frac{\partial p}{\partial y} + \nu(\frac{\partial^2 v_y}{\partial x^2} + \frac{\partial^2 v_y}{\partial y^2}) + g_y
\end{eqnarray}
\right.
\]
数値計算用に偏微分記号を置き換える(差分法)
ここからがようやく本題ですが,式を見るとまだまだ"暗号"(\( \partial \)記号)が残っています.このままコンピュータに微小の概念を教えることは困難です. というか,そもそもナビエ・ストークス方程式自体がまだ数学的に解けていないのだから数値計算というゴリ押しな手段しかとれないのです.具体的にどうするのかという話ですが,考え方はとてもシンプルです.式の中で"微小"となっている部分を"十分に小さい数字"として扱うというだけです. 当然,計算誤差は発生します.その点も十分に考慮する必要はありますが,今回は細かく説明はしません.普通に難しいからです(私もよく分りません).
ここで,微分の定義を思い出してみてください.
\[
\frac{df(x)}{dx} = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}
\]
このとき\( \Delta x \)が十分に小さければそのまま極限を外して近似することができます.
\[
\frac{df(x)}{dx} \approx \frac{f(x + \Delta x) - f(x)}{\Delta x}
\]
2階微分もやってみましょう.
\[
\begin{align}
\frac{d^2f(x)}{dx^2} &= \lim_{\Delta x \to 0} \frac{ \frac{f(x + 2 \Delta x) - f(x + \Delta x)}{\Delta x} - \frac{f(x + \Delta x) - f(x)}{\Delta x}}{\Delta x} \\
&= \lim_{\Delta x \to 0} \frac{f(x + 2 \Delta x) - 2 f(x + \Delta x) + f(x)}{\Delta x^2} \\
&\approx \frac{f(x + 2 \Delta x) - 2 f(x + \Delta x) + f(x)}{\Delta x^2}
\end{align}
\]
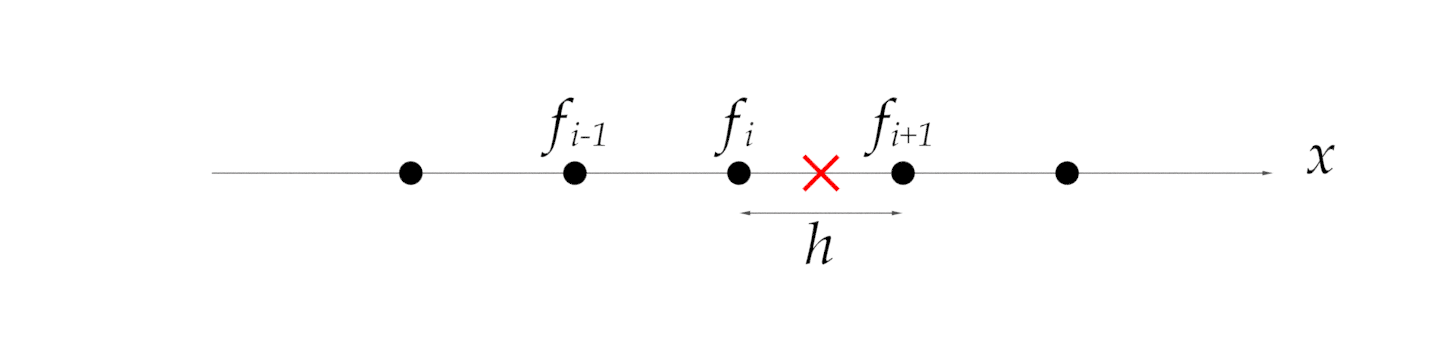
実際には\( f(x) \)の部分に流速\( \vec{v} \)や圧力\( p \)が入ってきますが,数値計算時は連続的な関数ではなく離散データとして扱います.また,それぞれの間隔を等しいものとして扱い,間隔\( h \)とします. このため,表記を以下のように変えてやります.何番目の位置かを示す添え字を右下につけています.プログラミングでいうところの配列みたいなイメージです.
\[
\frac{df(x)}{dx} \approx \frac{f_{i+1} - f_i}{h} (前進差分近似)
\]
上式は前進差分近似と呼ばれ,上図の×印部分の微分係数を近似しています.また,後ろ側の微分係数で近似したものを後進差分近似, 2倍分の幅をとって中心部分の微分係数で近似する中心差分近似があります.まあ近似の仕方には色々方法があるってことですね.
\[
\frac{df(x)}{dx} \approx \frac{f_i - f_{i-1}}{h} (後進差分近似)\\
\frac{df(x)}{dx} \approx \frac{f_{i+1} - f_{i-1}}{2h} (中心差分近似)
\]
2階微分も同様に表記してみましょう.これについては大体以下の式で近似することが多いです.
\[
\frac{d^2f(x)}{dx^2} \approx \frac{f_{i+1} - 2f_i + f_{i-1}}{h^2}
\]
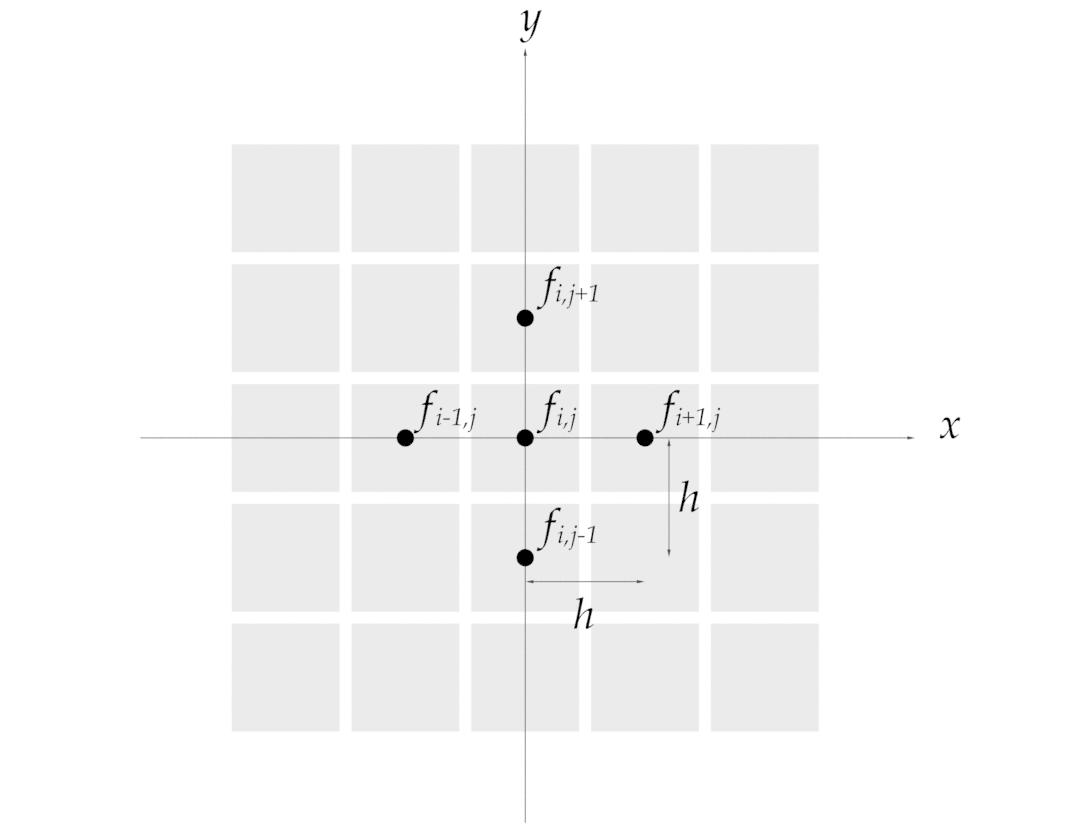
次は2次元空間を考えてみましょう.これも少し表記を変えてやるだけです.
1階偏微分
\[
\frac{\partial f}{\partial x} \approx \frac{f_{i+1, j} - f_{i, j}}{h}, \ \frac{\partial f}{\partial y} \approx \frac{f_{i, j+1} - f_{i, j}}{h} (前進差分近似)\\
\frac{\partial f}{\partial x} \approx \frac{f_{i, j} - f_{i-1, j}}{h}, \ \frac{\partial f}{\partial y} \approx \frac{f_{i, j} - f_{i, j-1}}{h} (後進差分近似)\\
\frac{\partial f}{\partial x} \approx \frac{f_{i+1, j} - f_{i-1, j}}{2h}, \ \frac{\partial f}{\partial y} \approx \frac{f_{i, j+1} - f_{i, j-1}}{2h} (中心差分近似)\\
\]
2階偏微分
\[
\frac{\partial^2 f}{\partial x^2} \approx \frac{f_{i+1, j} - 2f_{i, j} + f_{i-1, j}}{h^2},\ \frac{\partial^2 f}{\partial y^2} \approx \frac{f_{i, j+1} - 2f_{i, j} + f_{i, j-1}}{h^2}
\]
こうすることで,"暗号"(\( \partial \)記号)を"四則演算で計算可能な式"に置き換えることできます.色々添え字はついていますが全て具体的な数で計算できることがわかると思います. 実際,上の式は公式として暗記してもいいくらいよく使うのでしっかり理解しておいてください.
あとはナビエ・ストークス方程式の偏微分記号を上式を用いて機械的に置き換えてやるだけで差分近似できます.
しかし,先に述べたように差分法による近似は必ず誤差が発生します.実際に絶えず流向が変わるような計算を行うときには,上式で近似するとうまくいかないそうなのです. そこでもう一工夫する必要があります.
まあ難しいことはさておき,先人達がうまくいかないと言っているのだから先人の真似をしたいと思います.そこで登場するのが,河村・桑原スキームと呼ばれる流体解析に特化した近似法です.
ナビエ・ストークス方程式に登場する以下の項は次のように置き換えましょう.
\[
\begin{align}
v_x \frac{\partial f}{\partial x} & \approx \frac{-f_{i+2, j} + 8(f_{i+1, j} - f_{i-1, j}) + f_{i-2, j}}{12h} \\
& + |f_{i,j}| \cdot \frac{f_{i+2, j} - 4f_{i+1, j} + 6f_{i, j} - 4f_{i, j-1} + f_{i-2, j}}{4h} \\
v_y \frac{\partial f}{\partial y} & \approx \frac{-f_{i, j+2} + 8(f_{1, j+1} - f_{i, j-1}) + f_{i, j-2}}{12h} \\
& + |f_{i,j}| \cdot \frac{f_{i, j+2} - 4f_{i, j+1} + 6f_{i, j} - 4f_{i, j-1} + f_{i, j-2}}{4h}
\end{align}
\]
ごちゃごちゃした式に見えますが大体の意味を汲み取ると,下流よりも上流の方が場に与える影響が大きいだろうという仮定の下,式中の絶対値部分で流向を自動的に判別してうまいこと計算するようです.
さて,お待たせしました.ナビエ・ストークス方程式を差分近似していきましょう.\( x \)成分について差分近似するとこうなります.
\[
\begin{align}
\frac{v^{(n+1)}_{x \ i, j} - v^{(n)}_{x \ i, j}}{\Delta t} &+ v^{(n)}_{x \ i, j} \cdot \frac{-v^{(n)}_{x \ i+2, j} + 8(v^{(n)}_{x \ i+1, j} - v^{(n)}_{x \ i-1, j}) + v^{(n)}_{x \ i-2, j}}{12h} \\
&+ |v^{(n)}_{x \ i, j}| \cdot \frac{v^{(n)}_{x \ i+2, j} - 4v^{(n)}_{x \ i+1, j} + 6v^{(n)}_{x \ i, j} - 4v^{(n)}_{x \ i-1, j} + v^{(n)}_{x \ i-2, j}}{4h} \\
&+ v^{(n)}_{y \ i, j} \cdot \frac{-v^{(n)}_{x \ i, j+2} + 8(v^{(n)}_{x \ i, j+1} - v^{(n)}_{x \ i, j-1}) + v^{(n)}_{x \ i, j-2}}{12h} \\
&+ |v^{(n)}_{y \ i, j}| \cdot \frac{v^{(n)}_{x \ i, j+2} - 4v^{(n)}_{x \ i, j+1} + 6v^{(n)}_{x \ i, j} - 4v^{(n)}_{x \ i, j-1} + v^{(n)}_{x \ i, j-2}}{4h}
\end{align}
\]
\[
\begin{align}
&= - \frac{1}{\rho} \cdot \frac{p^{(n)}_{i+1, j} - p^{(n)}_{i-1, j}}{2h} \\
&+ \nu ( \frac{v^{(n)}_{x \ i+1, j} - 2v^{(n)}_{x \ i, j} + v^{(n)}_{x \ i-1, j}}{h^2} + \frac{v^{(n)}_{x \ i, j+1} - 2v^{(n)}_{x \ i, j} + v^{(n)}_{x \ i, j-1}}{h^2}) \\
&+ g_x
\end{align}
\]
これはひどい.しかも前置き無しに,しれっとまた新しい表記法で記述しています.文字右上の添え字は計算ステップ回数を示しています.つまり\( (n) \)とついている数は既知の古い値で, \( (n+1) \)とついている数はこれから知りたい未知の値ということです.
これから知りたい未知の値\( v^{(n+1)}_{x \ i, j} \)について解いて少し整理します.
\[
\begin{align}
v^{(n+1)}_{x \ i, j} &= v^{(n)}_{x \ i, j} \\
&- \Delta t \\
&\cdot \{ v^{(n)}_{x \ i, j} \cdot \frac{-v^{(n)}_{x \ i+2, j} + 8(v^{(n)}_{x \ i+1, j} - v^{(n)}_{x \ i-1, j}) + v^{(n)}_{x \ i-2, j}}{12h} \\
&+ |v^{(n)}_{x \ i, j}| \cdot \frac{v^{(n)}_{x \ i+2, j} - 4v^{(n)}_{x \ i+1, j} + 6v^{(n)}_{x \ i, j} - 4v^{(n)}_{x \ i-1, j} + v^{(n)}_{x \ i-2, j}}{4h} \\
&+ v^{(n)}_{y \ i, j} \cdot \frac{-v^{(n)}_{x \ i+2, j} + 8(v^{(n)}_{x \ i+1, j} - v^{(n)}_{x \ i-1, j}) + v^{(n)}_{x \ i-2, j}}{12h} \\
&+ |v^{(n)}_{y \ i, j}| \cdot \frac{v^{(n)}_{x \ i+2, j} - 4v^{(n)}_{x \ i+1, j} + 6v^{(n)}_{x \ i, j} - 4v^{(n)}_{x \ i-1, j} + v^{(n)}_{x \ i-2, j}}{4h} \} \\
&- \frac{\Delta t}{2 \rho h}(p^{(n)}_{i+1, j} - p^{(n)}_{i-1, j}) \\
&+ \frac{\nu \Delta t}{h^2} (v^{(n)}_{x \ i+1, j} + v^{(n)}_{x \ i-1, j} + v^{(n)}_{x \ i, j+1} + v^{(n)}_{x \ i, j-1} - 4v^{(n)}_{x \ i, j}) \\
&+ g_x \Delta t
\end{align}
\]
\( y \)成分も同様に,\( v^{(n+1)}_{y \ i, j} \)について解きます.
\[
\begin{align}
v^{(n+1)}_{y \ i, j} &= v^{(n)}_{y \ i, j} \\
&- \Delta t \\
&\cdot \{ v^{(n)}_{x \ i, j} \cdot \frac{-v^{(n)}_{y \ i, j+2} + 8(v^{(n)}_{y \ i, j+1} - v^{(n)}_{y \ i, j-1}) + v^{(n)}_{y \ i, j-2}}{12h} \\
&+ |v^{(n)}_{x \ i, j}| \cdot \frac{v^{(n)}_{y \ i, j+2} - 4v^{(n)}_{y \ i, j+1} + 6v^{(n)}_{y \ i, j} - 4v^{(n)}_{y \ i, j-1} + v^{(n)}_{y \ i, j-2}}{4h} \\
&+ v^{(n)}_{y \ i, j} \cdot \frac{-v^{(n)}_{y \ i, j+2} + 8(v^{(n)}_{y \ i, j+1} - v^{(n)}_{y \ i, j-1}) + v^{(n)}_{y \ i, j-2}}{12h} \\
&+ |v^{(n)}_{y \ i, j}| \cdot \frac{v^{(n)}_{y \ i, j+2} - 4v^{(n)}_{y \ i, j+1} + 6v^{(n)}_{y \ i, j} - 4v^{(n)}_{y \ i, j-1} + v^{(n)}_{y \ i, j-2}}{4h} \} \\
&- \frac{\Delta t}{2 \rho h}(p^{(n)}_{i, j+1} - p^{(n)}_{i, j-1}) \\
&+ \frac{\nu \Delta t}{h^2} (v^{(n)}_{y \ i+1, j} + v^{(n)}_{y \ i-1, j} + v^{(n)}_{y \ i, j+1} + v^{(n)}_{y \ i, j-1} - 4v^{(n)}_{y \ i, j}) \\
&+ g_y \Delta t
\end{align}
\]
おめでとうございます.これであなたは未来の流速を予測することが可能になりましたね.
圧力場を更新する
---【2020/5/29追記】
以下の説明はナビエ・ストークス方程式を無次元化した場合の話です.ここまでの流れで無次元化には一切触れていなかったのでのですが,これを書いた後で以下の式が無次元化した場合の式であることに気づいてしまいました. ということで,順番が入れ替わってしまいますが,まずはナビエ・ストークス方程式の無次元化について先に読んで頂けると幸いです.
読みづらい構成で申し訳ないですが,何らかの形で修正したいと考えております(といいつつ放置するパターン).
---
ついにここまで来てしまいました,実はここが最難関項目です.まだ1つ未知関数\( p \)が残っています.上式を見るとナビエ・ストークス方程式を差分近似しただけでは圧力\( p \)を更新できないことがわかります.
式中に\( p^{(n+1)} \)という項が1つも出てこないのですから当然ですね.実はこの圧力\( p \)が方程式の取り扱いを本質的に難しくしている要因の1つのなのです.私もここで一度挫折しました.
まずは圧力\( p \)を決めるための条件を定義しましょう.思い出してください,序盤でナビエ・ストークス方程式の"おまけ"としてついていたもう1つの式をここで使用します.
\[
\nabla \cdot \vec{v} = 0
\]
上式は流速場の発散が0ということで,"流体が非圧縮だ"ということを表しています.この式をナビエ・ストークス方程式とうまいこと組み合わせて計算すると以下の式が導出されるんだそうです. この辺も普通に難しいので説明はしません(できません).詳しくは圧力ポアソン方程式でググってみてください.
とは言え,あまりにも投げやり過ぎたので解説ページを作りました.詳しい情報はこちらをご覧ください.
\[
\nabla^2 p = - \{ ( \frac{\partial v_x}{\partial x} )^2 + ( \frac{\partial v_y}{\partial y} )^2 + 2 \frac{\partial v_x}{\partial y} \frac{\partial v_y}{\partial x} \}
\]
ただし,上式は簡単のため外力\( \vec{g} \)をゼロとして扱った場合の式です.導出の過程を理解していないので,外力がどう効いてくるのかは要確認ですね(適当な説明で申し訳ない).
ではこの式をどうやって使用するのかという話ですが,残念ながらこれもまた一筋縄ではいきません.まずはこの式の役割について理解してみましょう.
流速については既知の流速場と圧力場から1ステップ先の状態を知ることができていますが,圧力についてはまだ値が更新されず1ステップ分取り残されている状態です. 上式は計算済みの新しい流速場の情報を用いて古い情報の圧力場をいい感じに修正するという役割を持っています.
また,上式には時間\( t \)が含まれていないので定常的な振る舞いをします.つまり再帰的に\( p \)を更新しながら計算をブン回すとある一定の状態に収束します.
ある程度\( p \)が収束したら計算を切り上げて,新しい\( p^{(n+1)} \)としてやります.これが大まかな計算の流れです.
では計算方法についてです.まずは上式の∇を展開します.
\[
\frac{\partial^2 p}{\partial x^2} + \frac{\partial^2 p}{\partial y^2} = - \{ ( \frac{\partial v_x}{\partial x} )^2 + ( \frac{\partial v_y}{\partial y} )^2 + 2 \frac{\partial v_x}{\partial y} \frac{\partial v_y}{\partial x} \}
\]
差分近似します.このとき,流速は新しい情報を用いるので\( \vec{v}^{(n+1)} \)とします.
\[
\begin{align}
& \frac{p^{(n)}_{i+1, j} - 2 p^{(n)}_{i, j} + p^{(n)}_{i-1, j}}{h^2} + \frac{p^{(n)}_{i, j+1} - 2 p^{(n)}_{i, j} + p^{(n)}_{i, j-1}}{h^2} \\
= & - \{ (\frac{v^{(n+1)}_{x \ i+1, j} - v^{(n+1)}_{x \ i-1, j}}{2h})^2 + (\frac{v^{(n+1)}_{y \ i, j+1} - v^{(n+1)}_{y \ i, j-1}}{2h})^2 \\
& + 2 \cdot \frac{v^{(n+1)}_{x \ i, j+1} - v^{(n+1)}_{x \ i, j-1}}{2h} \cdot \frac{v^{(n+1)}_{y \ i+1, j} - v^{(n+1)}_{y \ i-1, j}}{2h} \} \\
& + (\frac{v^{(n+1)}_{x \ i+1, j} - v^{(n+1)}_{x \ i-1, j}}{2h} + \frac{v^{(n+1)}_{y \ i, j+1} - v^{(n+1)}_{y \ i, j-1}}{2h}) / \Delta t
\end{align}
\]
そして差分近似しただけかと思いきや,またしれっと一番最後の行に補正項を追加しています.これを追加しないと流体としてはおかしい振る舞いをしてしまうそうなのです. この辺は計算誤差をしっかり考えないと出てこない項なので,あまり気にせずこのまま進みます.
\( p^{(n)}_{i, j} \)について解いて少し整理します.
\[
\begin{align}
p^{(n)}_{i, j} & = \frac{1}{4} \cdot (p^{(n)}_{i+1, j} + p^{(n)}_{i-1, j} + p^{(n)}_{i, j+1} + p^{(n)}_{i, j-1}) \\
& + \frac{h}{8} \{ (v^{(n+1)}_{x \ i+1, j} - v^{(n+1)}_{x \ i-1, j})^2 + (v^{(n+1)}_{x \ i, j+1} - v^{(n+1)}_{x \ i, j-1})^2 \\
& + \frac{1}{h} (v^{(n+1)}_{x \ i, j+1} - v^{(n+1)}_{x \ i, j-1}) (v^{(n+1)}_{y \ i+1, j} - v^{(n+1)}_{y \ i-1, j}) \} \\
& - \frac{h}{8 \Delta t}(v^{(n+1)}_{x \ i+1, j} - v^{(n+1)}_{x \ i-1, j} + v^{(n+1)}_{y \ i, j+1} - v^{(n+1)}_{y \ i, j-1})
\end{align}
\]
あとはすべての点において\( p \)が収束するまで上式を用いて\( p \)を更新し続けます.\( p \)を更新するタイミングですが,全ての計算結果をストックして一周した後に一気に更新しても良いし,逐一\( p \)を更新しながら次の点の計算を始めても良いです. ちなみに前者は,ヤコビ法,後者をガウス=ザイデル法と呼びます.
いいところで計算を切り上げたら,計算で得られた圧力場\( p \)を\( p^{(n+1)} \)としましょう.おつかれさまでした.これで流体の未来を完璧に予測することが可能になりました.
初期条件・境界条件
微分方程式を解くには初期条件と境界条件が必要で,数値解析においても同様です.これらの条件を適切に設定することは, 場の計算と同じくらい重要で全体の挙動に大きく影響を与えます.初期条件については容易に想像できると思います.静止した状態からスタートするのか,流れがある状態からスタートするのか最初に決めてやればよいだけなので簡単なことです.
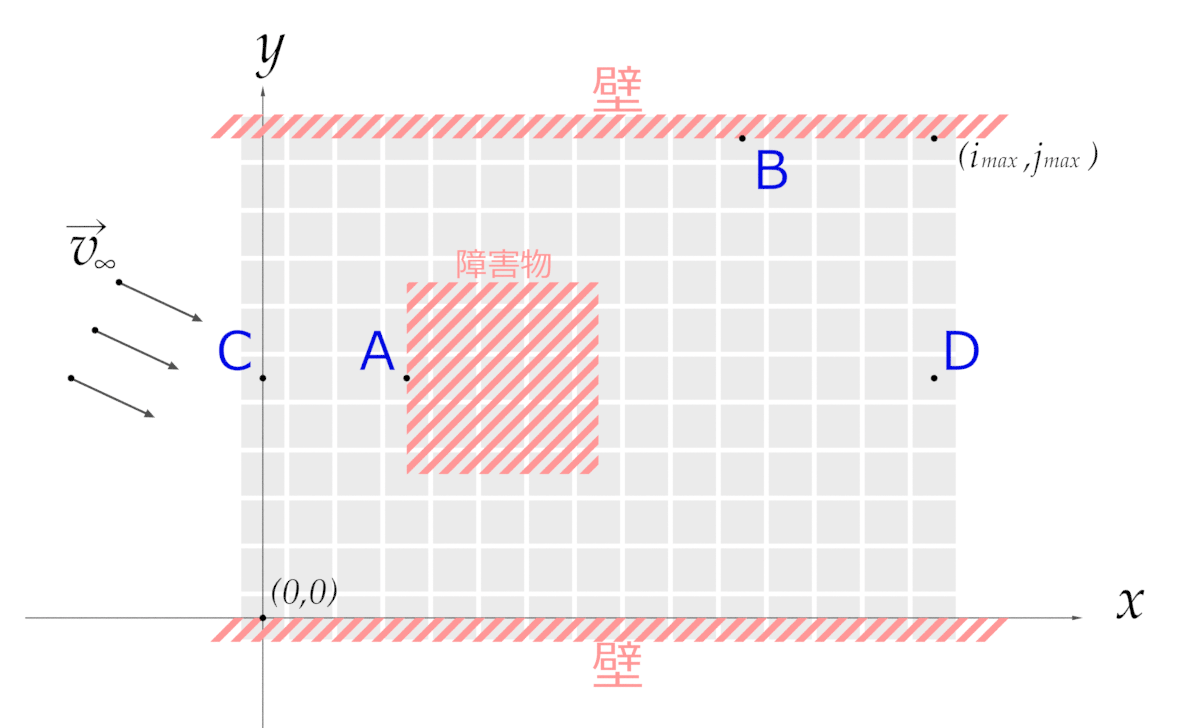
もう一方の境界条件とは具体的に言えば,"周りは壁で囲まれているのか","端から流入したり流出する出口があるのか","障害物が配置されているのか",等の条件のことです.
ということで,今回は下図のような条件を考えていきたいと思います.
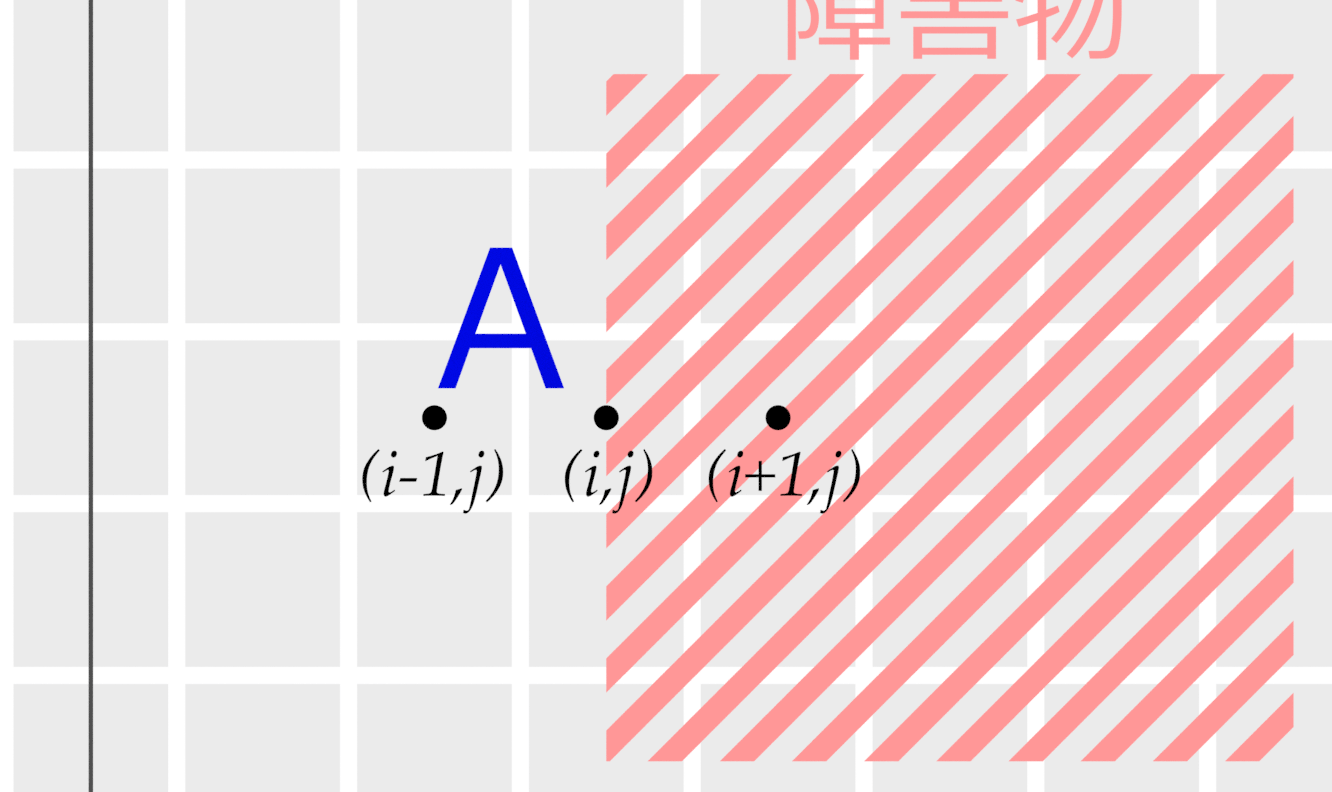
まずはAから見ていきます.障害物との境界部分\( (i, j) \)について圧力\( p \)と流速\( \vec{v} \)をそれぞれ定義する必要があります. また,流速\( \vec{v} \)については河村・桑原スキームを使用しているので,境界部分よりさらに1つ内側の\( (i+1, j) \)についても考える必要があります.
圧力\( p_{i, j} \)については壁の手前にかかっていた圧力をそのままかけてやります.また,境界部分の流速\( \vec{v}_{i, j} \)についてはゼロとします.この辺の定義は水理学をかじってないとイメージしづらいかもしれませんが, ここではそういうもんだということにしておいてください.
問題は壁の中の流速\( \vec{v}_{i+1, j} \)はどうやって定義するのかという話ですが,当然壁の中には流速は存在しないので仮想的な流速を定義する必要があります. 壁の手前では\( \vec{v}_{i-1, j} \)の流速があって,境界部分では\( \vec{0}\)へと変化しています.このまま流速が線形的に変化するとすれば\( \vec{v}_{i, j} \) = \( - \vec{v}_{i-1, j} \)になると言えます. これが基本的な考え方ですが,より直感的なイメージとしては壁の内側にめり込むほどそれを阻止するためにめり込んだ距離に応じて逆方向の流速が発生するといったところでしょうか.
\[
\begin{align}
p_{i, j} & = p_{i-1, j} \\
\vec{v}_{i, j} &= \vec{0} \\
\vec{v}_{i+1, j} &= - \vec{v}_{i-1, j}
\end{align}
\]
次にBです.考え方はAと同じで以下のように定義します.
\[
\begin{align}
p_{i, j_{max}} & = p_{i, j_{max}-1} \\
\vec{v}_{i, j_{max}} &= \vec{0} \\
\vec{v}_{i, j_{max}+1} &= - \vec{v}_{i, j_{max}-1}
\end{align}
\]
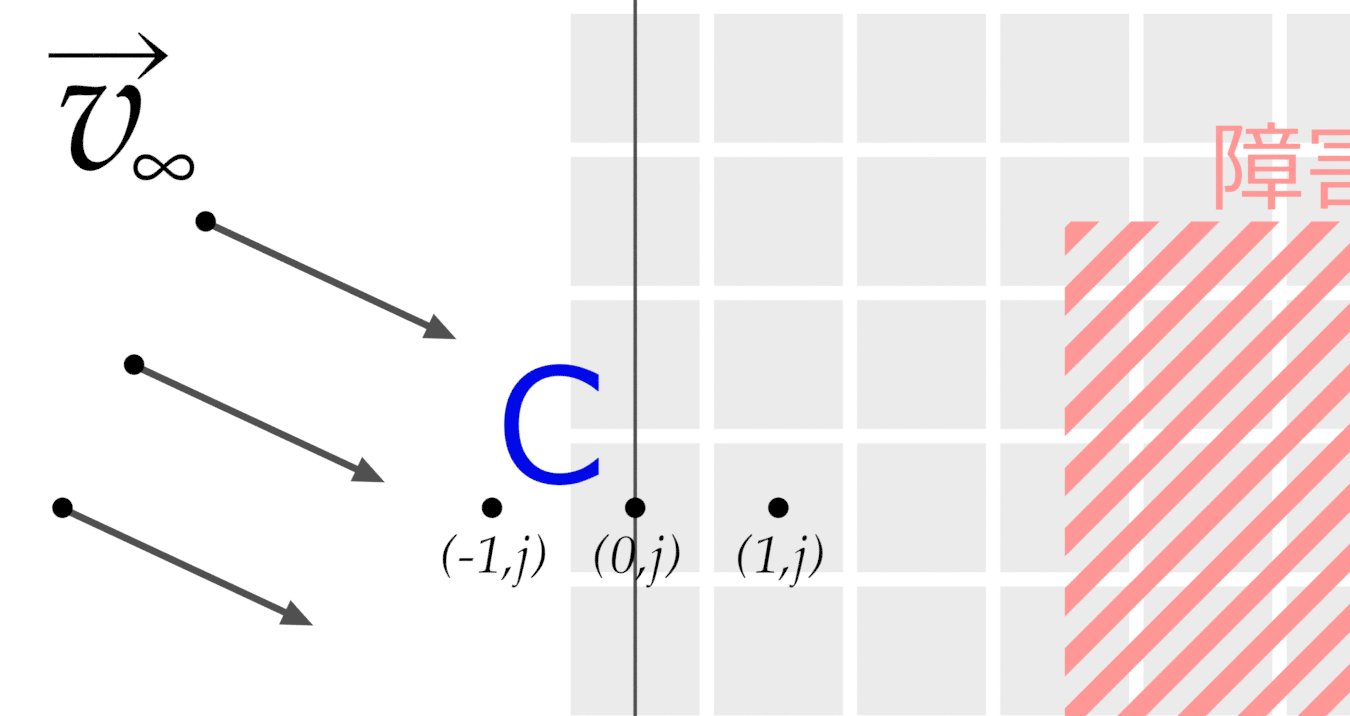
続いてCです.計算領域の外は一様な流速\( \vec{v}_{\infty} \)とします.前述した通り,ナビエ・ストークス方程式では圧力の大小に関わらず近傍との圧力の差のみが影響します. このことから,流入部の圧力\( p_{0, j} \)は任意の値でよいのですが特に理由はないのでゼロとしています.ただし,この流入部の圧力が基準の値となるので,初期の圧力や流出部の圧力を定義する際にこの辺を意識する必要があります.
流入部の流速\( \vec{v}_{0, j} \)と\( \vec{v}_{-1, j} \)はそのまま\( \vec{v}_{\infty} \)とします.
\[
\begin{align}
p_{0, j} & = 0 \\
\vec{v}_{0, j} &= \vec{v}_{\infty} \\
\vec{v}_{-1, j} &= \vec{v}_{\infty}
\end{align}
\]
最後にDです.基本的な考え方は流出部付近の流速,圧力の情報を用いて流出部の値を1次近似して予想するというものです. 式を見ると難しそうに見えますが,理屈は簡単です.ただし,圧力\( p_{i_{max}, j} \)については,簡略化のため流入部と同じゼロとしています.もちろん丁寧に1次近似してやるのも良しです.
\[
\begin{align}
p_{i_{max}, j} & = 0 \ (または、\ p_{i_{max}, j} = 2 p_{i_{max}-1, j} - p_{i_{max}-2, j} )\\
\vec{v}_{i_{max}, j} &= 2 \vec{v}_{i_{max}-1, j} - \vec{v}_{i_{max}-2, j} \\
\vec{v}_{i_{max}+1, j} &= 2 \vec{v}_{i_{max}, j} - \vec{v}_{i_{max}-1, j}
\end{align}
\]
単位の扱いと無次元化
ナビエ・ストークス方程式には圧力場,流速場の他にいくつかの定数があります.実際に計算をする際に,広く知られている定数等を引用するときには単位について考慮する必要があります.――単位は大事例えば,今回出てきた変数・定数の単位は以下のように扱います.
\[
\begin{align}
\Delta t &: [s] \\
h &: [m] \\
\rho &: [kg / m^3] \\
\mu &: [kg \cdot m^{-1} \cdot s^{-1}] \\
( \frac{\mu}{\rho} = ) \nu &: [m^2 / s] \\
\vec{g} &: [kg \cdot m \cdot s^{-2}] \\
\vec{v} &: [m / s] \\
p &: [kg \cdot m^{-1} \cdot s^{-2}]
\end{align}
\]
ここで大事なことは,長さは\( [m] \),質量は\( [kg] \),時間は\( [s] \)に全て統一しているということです.計算を行うときは全ての変数・定数の単位を一度分解して揃える必要があります. 例えば,これらの中に1つだけ\( [cm] \)を混ぜて計算するのはダメってことです.これを意識しないと色々おかしなことになります.
ちなみに長さは\( [m] \),質量は\( [kg] \),時間は\( [s] \)といった統一方法はSI単位の中のMKS単位系と呼ばれ国際基準としてよく使われています.
ただし,こんなの全部考えるの面倒くさいという場合はナビエ・ストークス方程式の無次元化という方法があります.
上記で登場する複数の定数を組み合わせて,定数の数をコンパクトに1つまで絞ってしまうという方法です.これにより,流体の性質を"レイノルズ数\( (Re) \)"という1つの定数で記述することができます. レイノルズ数は無次元の値で単位を持ちません.敢えて単位を記述するなら\( [1] \)と表記できます.
このレイノルズ数は流体の挙動を決める定数として色々なところで頻出するワードなので知っておいてもいいかもしれないですね.
そして,以下が無次元化したナビエ・ストークス方程式です.コンパクトになりましたね.
\[
\frac{\partial \vec{v}}{\partial t} + (\vec{v} \cdot \nabla) \vec{v} = - \nabla p + \frac{1}{Re} \nabla^2 \vec{v} + \vec{g}
\]
無次元化するもう1つのメリットとしては,スケールや,時間等の規模に関わらずレイノルズ数さえ揃えておけば流体の挙動が同じになるということです. これは風洞実験などでミニチュアの模型を作成するときに,実際の挙動を再現するために流速を調整してレイノルズ数を揃えるといった様に上記の手法をとることもあります.
最後に
今回は,一通り流体シミュレーションを実装するための手法について解説を行いました.しかし自分の中でもまだ理解が足りていない部分が多く,「これ合ってるのか?」って思うところも正直あります. 動かした結果,何となく見た目はそれっぽくなっているので,とりあえず自分の中での目標は達成しましたが,この結果が科学的に信頼できるものなのかと訊かれれば疑問もあります.もし,この情報を研究等に用いるのであれば(そんな人がわざわざこんなページ見に来ないと思うけど)一度しっかりリサーチしてください.特に計算精度についてはかなり慎重に考慮しないといけない部分なのでしっかり検証してください.
その他,間違い・ご指摘等がありましたらご連絡ください.