キーワード
図形の特徴をざっくり割り出す式
今回ご紹介するのはこちらの式です.(唐突な新コーナー)\[
K = \frac{l^2}{4 \pi A}
\]
何か図形が1つあったとして,その図形に対して\( K \)の値が決まります.ここで,\( A \)は面積,\( l \)は周の長さです.簡単ですね.
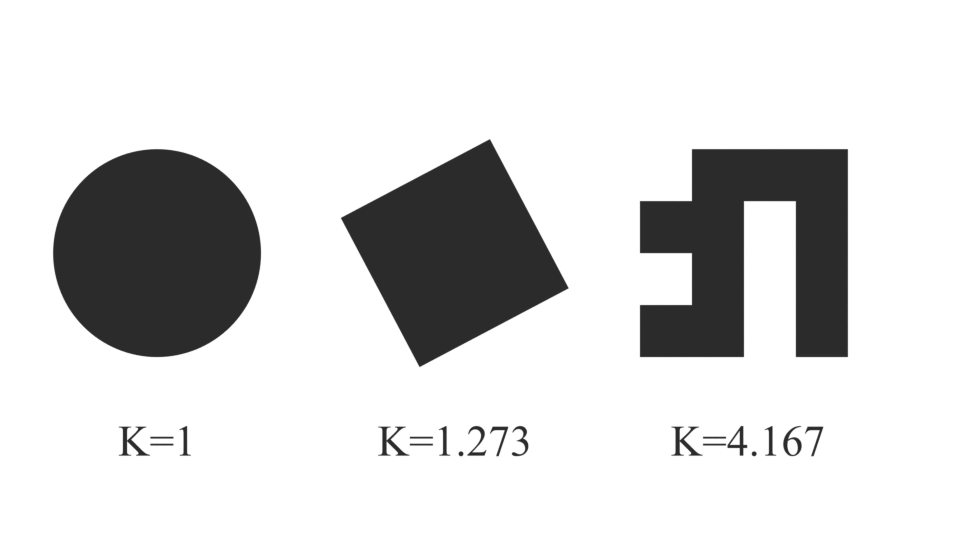
この式は図形の複雑さを示しています.複雑な図形では\( K \)が大きくなります.逆に円のような単純な図形では\( K \)が小さくなります.
世の中には様々な図形がありますが,\( K \)を求めるだけで図形が持つ固有の値を知ることができます.もちろん\( K \)を求めるだけで全ての 図形を識別することはできませんが,この図形はなんか丸っぽいなあとか,そんなざっくりした識別は可能なのです.
さて,ここで少しこの式を眺めてみましょう.変数は\( A \)と\( l \)の2つのみで単純に周長と面積の比という関係になります. \( l \)を2乗しているのは分母と分子の次元を揃えることで大きさの異なる相似な図形でも\( K \)の値を一定に保つためです.分母の\( 4 \pi \)は一体何かと言いますと,最も単純な図形である円 のときに\( K = 1 \)となるように調整するためのものです.
ラスタスキャンで周長と面積を求める
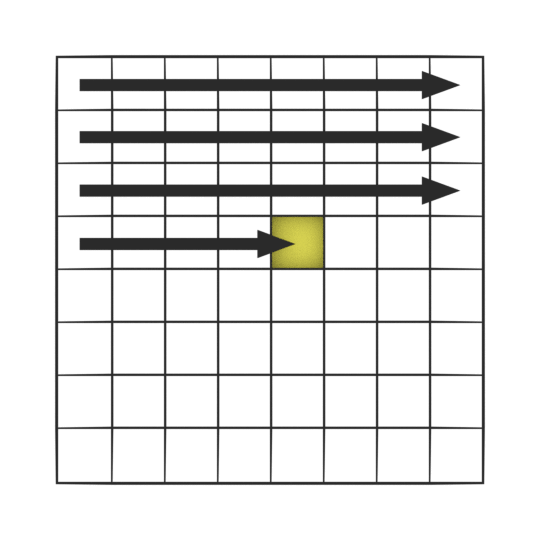
あとは,図形の周長と面積だけ求めてしまえば形状認識できるので,正直ここで話を終わらせてもよかったんですが, あまりにも投げやり感があったのでラスタスキャンによる簡単な算出アルゴリズムだけ紹介しときます.そもそもラスタスキャンとはどんなものかと言いますと,こんな図になります.
上図の格子は画像のセルだと思ってください.画像じゃなくても2次元配列なら何でもいいんですが,セルの中に色の情報が格納されています.このセルを順番に(一般的には左上から右向きに) 調べていきます.
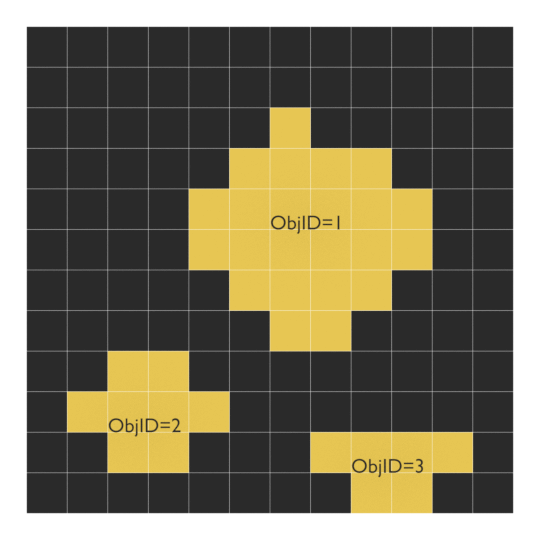
ここで,こんな2値化された画像があるとします.連続した黄色のセルを1つの物体と見なしてObjIDを割り当てます.実際にObjIDを割り当てるときは専用のBand領域(RGBのどれか,またはそれ以外)を用意しておき, その中にIDを格納しておくのがいいでしょう.
面積は簡単ですね,説明するまでもないですが,各ObjIDのセル数を数えるだけで求まります(下表).
| ObjID | A |
|---|---|
| 1 | 23 |
| 2 | 8 |
| 3 | 6 |
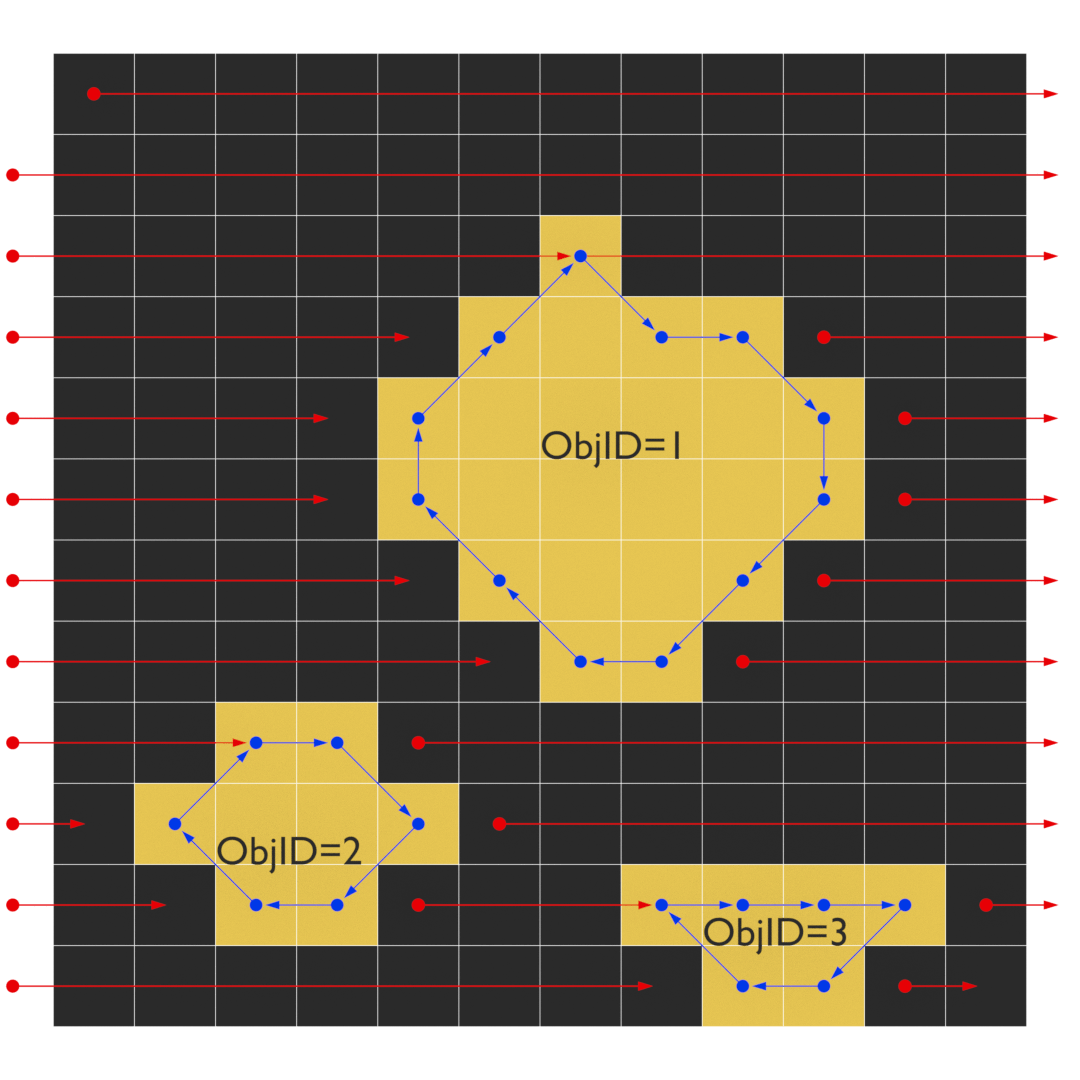
次に周の長さを求めます.少し面倒ですが,そこまで難しくはないです. まずは,下図のような経路でラスタスキャンしていきます.黄色セルにぶつかったときに赤の経路から 青の経路に切り替わってぐるっと外周を回ってまた赤の経路に戻るといった流れです. このとき,スキャン済みの領域は飛ばして次の地点からスキャンを開始します.
あとは,青矢印の長さを合計するだけで周長が算出できます. 青矢印は下図の8種類しか出てきません.これらの矢印にd1~d8までの番号をつけてベクトルとして定義してしまいます.
\[
\vec{d_1} = (-1, -1), \left| \vec{d_1} \right| = \sqrt{2} \\
\vec{d_2} = (0, -1), \left| \vec{d_2} \right| = 1 \\
\vec{d_3} = (1, -1), \left| \vec{d_3} \right| = \sqrt{2} \\
\vec{d_4} = (1, 0), \left| \vec{d_4} \right| = 1 \\
\vec{d_5} = (1, 1), \left| \vec{d_5} \right| = \sqrt{2} \\
\vec{d_6} = (0, 1), \left| \vec{d_6} \right| = 1 \\
\vec{d_7} = (-1, 1), \left| \vec{d_7} \right| = \sqrt{2} \\
\vec{d_8} = (-1, 0), \left| \vec{d_8} \right| = 1 \\
\]
ここでObjID:1を例に見てみましょう.
外周の経路は\( d_5, d_4, d_5, d_6, d_7, d_7, d_8, d_1, d_1, d_2, d_3, d_3 \)です.従って周長\( l_1 \)は
\[
\begin{align}
l_1 &= \left| \vec{d_5} \right| + \left| \vec{d_4} \right| +\left| \vec{d_5} \right| + \left| \vec{d_6} \right| + \left| \vec{d_7} \right| + \left| \vec{d_7} \right| + \left| \vec{d_8} \right| + \left| \vec{d_1} \right| + \left| \vec{d_1} \right| + \left| \vec{d_2} \right| + \left| \vec{d_3} \right| + \left| \vec{d_3} \right| \\
&= 2 \left| \vec{d_1} \right| + \left| \vec{d_2} \right| + 2 \left| \vec{d_3} \right| + \left| \vec{d_4} \right| + 2 \left| \vec{d_5} \right| + \left| \vec{d_6} \right| + 2 \left| \vec{d_7} \right| + \left| \vec{d_8} \right| \\
&= 8 \sqrt{2} + 4 \\
&= 15.3137
\end{align}
\]
同様に\( l_2, l_3 \)も求めると下表のようになります.
| ObjID | 外周の経路 | l |
|---|---|---|
| 1 | d5,d4,d5,d6,d7,d7,d8,d1,d1,d2,d3,d3 | 15.3137 |
| 2 | d4,d5,d7,d8,d1,d2 | 7.6569 |
| 3 | d4,d4,d4,d7,d8,d1 | 6.8284 |
面積と周長が求まったので,各オブジェクトの\( K \)値を求めます.
| ObjID | l | A | K |
|---|---|---|---|
| 1 | 15.3137 | 23 | 0.811 |
| 2 | 7.6569 | 8 | 0.583 |
| 3 | 6.8284 | 6 | 0.618 |
これで\( K \)が算出されました.めでたしめでたし.でもよく見てください. \( K \)の値がどれも理論最小値である1を下回っています.これはまずい.
原因は周長に対して面積を余分にとっているせいなんですねえ.思い出してください.周長を求めるときは8方向のベクトルを考慮しましたが面積は単純にセルの数を数えただけです.つまり下図のように余分に面積をとってしまっていたんですねえ.
ただし,今回はサンプル画像が極端に小さかったためにこのような問題が発生しましたが, 十分に大きく面積をとればこのような問題は回避できるでしょう.
一応ちゃんと計算してみる
リアルタイムでカメラに映る画像を処理する場合は, ここまで計算すると逆に処理が遅くなったりとデメリットになることもあるので妥協するのもアリだと思います. ですが,今回は計算が合っているのかちゃんと確認してみましょう.| ObjID | l | A | K |
|---|---|---|---|
| 1 | 15.3137 | 16 | 1.166 |
| 2 | 7.6569 | 4 | 1.166 |
| 3 | 6.8284 | 2 | 1.855 |
計算結果によるとObjID:1,2は全く同じ形状という意外な結果となりました.確かに見比べると形が似ていなくもない. とまあ,こんな感じです.役に立つかは知らん.
おわりに
穴が開いてる図形のときはどうするだって?穴なんて無視ですよ,細かいなあ.(位相幾何学的にはアレな発言)以上,簡易的な解説でした.昨今,流行っているAIがよくわからんって方でもこれくらいなら気軽に実装できる感じがしませんか.色々と詰めが甘いですが,何かの参考になれば幸いです. サンプルプロジェクトなりサンプルコードなり用意しておけばいいんですが,今回はなしです. 以前にC#で書いたことはあるんですが,作ったのが昔過ぎて今見返すと色々アレだったので.どうせサンプルコードだけ 貼ってても見ないでしょう?