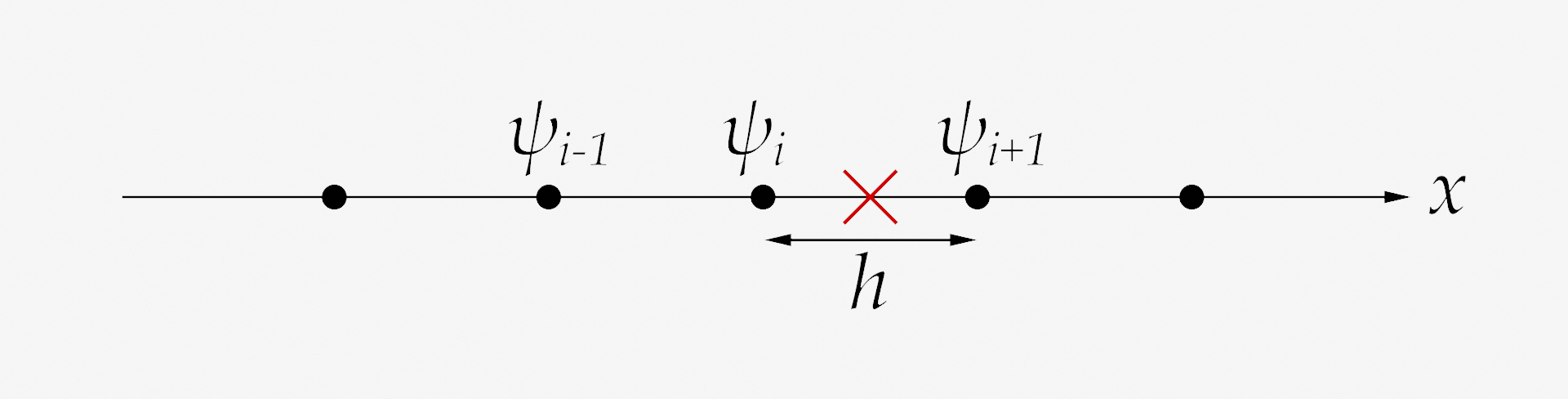キーワード
はじめに
ここでは偏微分方程式の数値解法(差分法)について,基本的な部分を一通り取り扱っていきます."微分"ではなく"偏微分"となっているのは, 空間が多次元であるということを意味しています(やや乱暴な言い方ですが).今回扱う方程式も,2次元以上の場合を考えていきます.偏微分方程式は,自然現象をシンプルに記述するための言語としてしばしば用いられます.流体の動き,熱伝導,電磁場,素粒子の挙動……のように,「ミクロな現象」から「マクロな現象」まで様々な例を挙げられます.
今回の目標は,簡単な偏微分方程式を数値解析して可視化することと,何か方程式を見たときに「これは何かこんな動きをしそう」といった感じに全体像を掴めるようになることです. (もちろん,どんな動きをするかは実際に計算しないとわからないのですが)
差分法の基本的な考え方
コンピュータ上で数値計算を実行するには,微分していようと何であろうと,まずは具体的な"数"として扱う必要があります. しかし,微分方程式には微小という概念があります.当然,以下の様な微分の記号が登場してきます.\[
\frac{\partial \psi}{\partial x}, \frac{\partial \psi}{\partial y}, \frac{\partial^2 \psi}{\partial x^2}, \frac{\partial^2 \psi}{\partial y^2}, \frac{\partial^3 \psi}{\partial x^3}, \cdots
\]
ここで\( \psi \)は何かの状態(密度,水深,圧力,…なんでも良い)を記述する未知関数だと思ってください.これらの記号をどのように取り扱っていくか考えていきます.
考え方は非常にシンプルです.式の中で"微小"となっている部分を"十分に小さい数字"として扱うというだけです. まずは微分の定義を思い出してみてください.微分とは,ある関数について,ある地点の「接線の傾き」(微分係数)を求めるものです.
\[
\frac{d \psi (x)}{dx} = \lim_{\Delta x \to 0} \frac{\psi(x + \Delta x) - \psi(x)}{\Delta x}
\]
このとき,\( \Delta x \)が十分に小さければそのまま極限を外して近似することができます.間隔が狭ければ,2点間の傾きは微分係数に一致するとみなせるということです.
\[
\frac{d \psi (x)}{dx} \approx \frac{\psi(x + \Delta x) - \psi(x)}{\Delta x}
\]
2階微分についても考えてみます.
\[
\begin{align}
\frac{d^2 \psi (x)}{dx^2} &= \lim_{\Delta x \to 0} \frac{ \frac{\psi(x + 2 \Delta x) - \psi(x + \Delta x)}{\Delta x} - \frac{\psi(x + \Delta x) - \psi(x)}{\Delta x}}{\Delta x} \\
&= \lim_{\Delta x \to 0} \frac{\psi(x + 2 \Delta x) - 2 \psi(x + \Delta x) + \psi(x)}{\Delta x^2} \\
&\approx \frac{\psi(x + 2 \Delta x) - 2 \psi(x + \Delta x) + \psi(x)}{\Delta x^2}
\end{align}
\]
数値計算時は連続的な関数ではなく離散データとして扱います.また,それぞれの間隔を等しいものとして扱い,間隔\( h \)とします. このため,表記を以下のように変えてやります.何番目の位置かを示す添え字を右下につけています.プログラミングでいうところの配列みたいなイメージです.
\[
\frac{d \psi (x_i)}{dx} \approx \frac{\psi_{i+1} - \psi_i}{h} (前進差分近似)
\]
\( x_i \)は\( i \)地点の\( x \)座標を示しています.よって\( \frac{d \psi (x_i)}{dx} \)は\( x_i \)地点の微分係数となります. 上式は前進差分近似と呼ばれ,上図の×印部分の微分係数を近似しています.\( i \)地点からちょっとずれてますね.近似計算なのでそこは大目に見てください.
また,後ろ側の微分係数で近似したものを後進差分近似,2倍分の幅をとって中心部分の微分係数で近似する中心差分近似があります.まあ近似の仕方には色々方法があるってことですね.
\[
\frac{d \psi(x_i)}{dx} \approx \frac{\psi_i - \psi_{i-1}}{h} (後進差分近似)\\
\frac{d \psi(x_i)}{dx} \approx \frac{\psi_{i+1} - \psi_{i-1}}{2h} (中心差分近似)
\]
2階微分についても同様に表記してみましょう.これについては大体以下の式で近似することが多いです.
\[
\frac{d^2\psi(x_i)}{dx^2} \approx \frac{\psi_{i+1} - 2\psi_i + \psi_{i-1}}{h^2}
\]
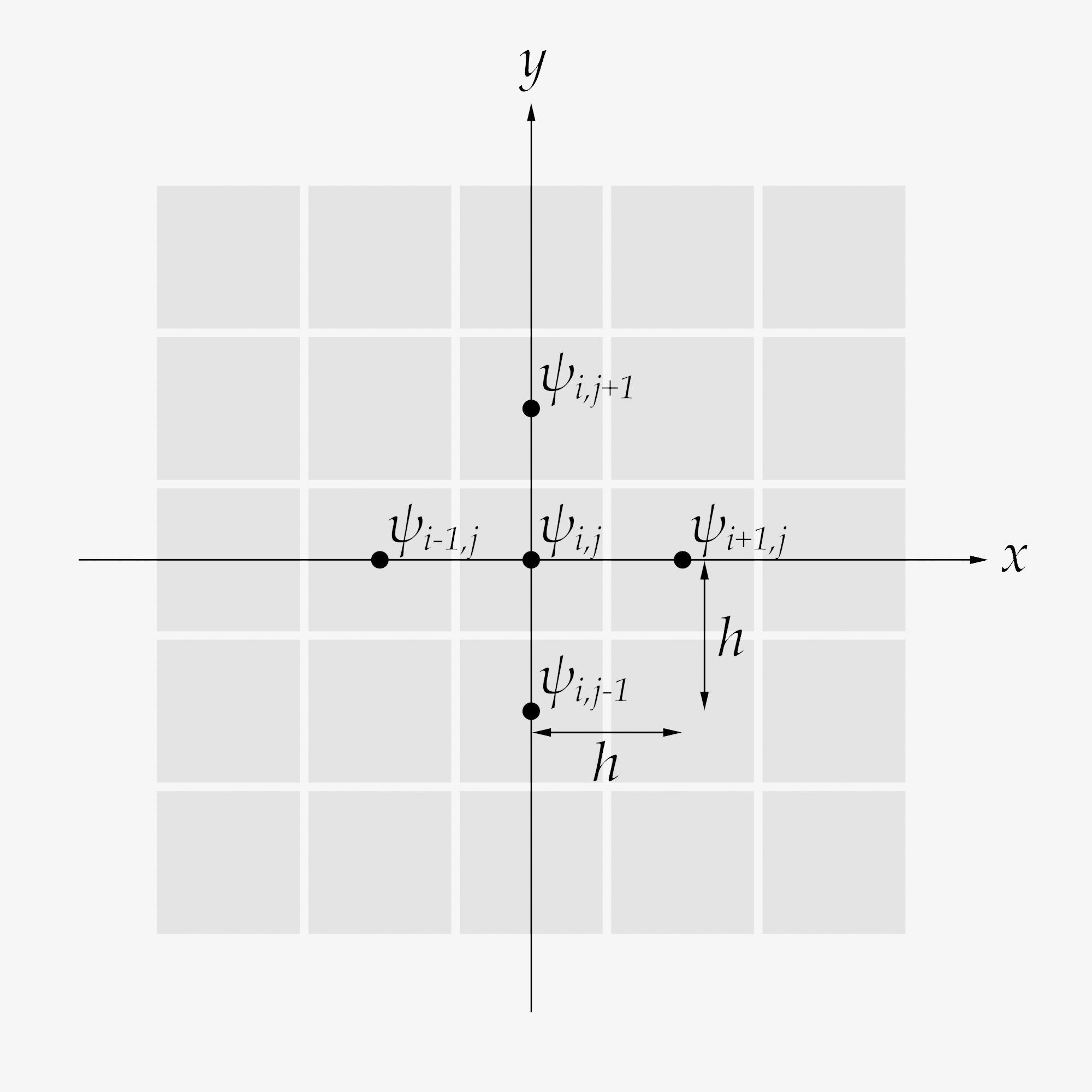
次は2次元空間を考えてみましょう.これも少し表記を変えてやるだけです.
1階偏微分
\[ \small{ \frac{\partial \psi(x_{i,j}, y_{i,j})}{\partial x} \approx \frac{\psi_{i+1, j} - \psi_{i, j}}{h}, \ \frac{\partial \psi(x_{i,j}, y_{i,j})}{\partial y} \approx \frac{\psi_{i, j+1} - \psi_{i, j}}{h} (前進差分近似)} \]
\[ \small{ \frac{\partial \psi(x_{i,j}, y_{i,j})}{\partial x} \approx \frac{\psi_{i, j} - \psi_{i-1, j}}{h}, \ \frac{\partial \psi(x_{i,j}, y_{i,j})}{\partial y} \approx \frac{\psi_{i, j} - \psi_{i, j-1}}{h} (後進差分近似)} \]
\[ \small{ \frac{\partial \psi(x_{i,j}, y_{i,j})}{\partial x} \approx \frac{\psi_{i+1, j} - \psi_{i-1, j}}{2h}, \ \frac{\partial \psi(x_{i,j}, y_{i,j})}{\partial y} \approx \frac{\psi_{i, j+1} - \psi_{i, j-1}}{2h} (中心差分近似)} \]
2階偏微分
\[
\small{
\frac{\partial^2 \psi(x_{i,j}, y_{i,j})}{\partial x^2} \approx \frac{\psi_{i+1, j} - 2\psi_{i, j} + \psi_{i-1, j}}{h^2}, \frac{\partial^2 \psi(x_{i,j}, y_{i,j})}{\partial y^2} \approx \frac{\psi_{i, j+1} - 2\psi_{i, j} + \psi_{i, j-1}}{h^2}
}
\]
こうすることで,\( \psi \)という複雑な関数の微分係数を単純な多項式で表現することができます.ある地点を考えるとき,近傍の状態が分かっていれば微分係数を計算することが可能になったということです.
差分法をより厳密に解釈してみる
前項では,直感的に理解しやすい説明をするために微分の定義から導出しましたが,計算誤差を評価するためにはもう少しだけ厳密な解釈が必要になってきます. 一般には,差分法で扱う近似式の導出はテイラー展開を用いることが多いです.この内容については最初からすべて理解する必要はないと思うので,わかる人だけついてきてください.(投げっぱなし)
ということで,何は無くともまずはテイラー展開です.\( \psi(x, y) \)について,\( x \)方向にテイラー展開していきます. 式が横に長くなり過ぎてしまうので,変数\( y \)の表記は省略させてください.
\[
\small{ \psi(x) = \psi_i + (x - x_i) \frac{\partial \psi(x_i)}{\partial x} + \frac{(x - x_i)^2}{2!} \frac{\partial^2 \psi(x_i)}{\partial x^2} + \frac{(x - x_i)^3}{3!} \frac{\partial^3 \psi(x_i)}{\partial x^3} + \cdots }
\]
ほとんど公式そのまんまなので難しくはないと思います.このように無限に続いていきます.テイラー展開によって導出された級数なので,\( \psi(x) \)が厳密にイコールで繋がっている状態です. このように一旦イコールで繋げるということは重要で,上記のように厳密な値を知っていれば計算する過程で色々(高次項とか)切り捨てた後に切り捨てた分の誤差を知ることができます.
ここで,上式に以下の数(条件)を代入します.
\[
x = x_{i+1} \longrightarrow \psi(x_{i+1}) = \psi_{i+1}
\]
\( x_{i+1} \)地点の微分係数\( \psi_{i+1} \)は,
\[
\psi_{i+1} = \psi_i + (x_{i+1} - x_i) \frac{\partial \psi(x_i)}{\partial x} + \frac{(x_{i+1} - x_i)^2}{2!} \frac{\partial^2 \psi(x_i)}{\partial x^2} + \cdots
\]
\( x_{i+1} - x_i = \Delta x = h \)なので,
\[
\psi_{i+1} = \psi_i + h \frac{\partial \psi(x_i)}{\partial x} + \frac{h^2}{2!} \frac{\partial^2 \psi(x_i)}{\partial x^2} + \cdots
\]
今回は2階微分までしか考えないので,3次以降の項は"誤差"とみなしてしまいます.このとき,この誤差は\( O(h^3) \)と表記します.\( O \)はオミクロンと読むそうです. 括弧の中の数は誤差のオーダーを示しています.オーダーとはとてもざっくりした表現です.定数倍の差なんてのは無視です.後程少しだけ触れるのでとりあえず"誤差だな"って思っててください.
\[
\psi_{i+1} = \psi_i + h \frac{\partial \psi(x_i)}{\partial x} + \frac{h^2}{2!} \frac{\partial^2 \psi(x_i)}{\partial x^2} + O(h^3)
\]
同様に\( \psi_{i-1} \)についても考えると以下のような式が導出されます.
\[
\psi_{i-1} = \psi_i - h \frac{\partial \psi(x_i)}{\partial x} + \frac{h^2}{2!} \frac{\partial^2 \psi(x_i)}{\partial x^2} + O(h^3)
\]
これら\( \psi_{i+1}, \psi_{i-1} \)の式には\( \psi \)の微分係数(1階微分,2階微分)の情報が含まれています. つまり,簡単な多項式を移項したりするだけで微分係数を求めることができます.
例えば,上記2本の式を組み合わせて\( \psi_{i+1} - \psi_{i-1} \)を計算してみます.
\[
\psi_{i+1} - \psi_{i-1} = 2h \frac{\partial \psi(x_i)}{\partial x} + O(h^3)
\]
移項して\( \frac{\partial \psi(x_i)}{\partial x} \)について解くと,
\[
\frac{\partial \psi(x_i)}{\partial x} = \frac{\psi_{i+1} - \psi_{i-1}}{2h} + O(h^2)
\]
誤差項\( O(h^2) \)から,「微分係数\( \frac{\partial \psi(x_i)}{\partial x} \)を\( h \)について,2次の精度で近似可能だ」といえることがわかります. おわかりいただけただろうか.下式は"1階微分の中心差分近似"そのものです.(お~すげ~)
\[
\frac{\partial \psi(x_i)}{\partial x} \approx \frac{\psi_{i+1} - \psi_{i-1}}{2h}
\]
続けて,\( \psi_{i+1} + \psi_{i-1} \)を計算してみます.
\[
\psi_{i+1} + \psi_{i-1} = 2 \psi_i + h^2 \frac{\partial^2 \psi(x_i)}{\partial x^2} + O(h^4)
\]
移項して\( \frac{\partial^2 \psi(x_i)}{\partial x^2} \)について解くと,
\[
\frac{\partial^2 \psi(x_i)}{\partial x^2} = \frac{\psi_{i+1} - 2 \psi_i + \psi_{i-1}}{h^2} + O(h^2)
\]
誤差項\( O(h^2) \)から,「2階微分の微分係数\( \frac{\partial^2 \psi(x_i)}{\partial x^2} \)を\( h \)について,2次の精度で近似可能だ」といえることがわかります. またまたおわかりいただけただろうか.下式は"2階微分の近似"になっています.
\[
\frac{\partial^2 \psi(x_i)}{\partial x^2} \approx \frac{\psi_{i+1} - 2 \psi_i + \psi_{i-1}}{h^2}
\]
"前進差分近似","後進差分近似"についても\( \psi_{i+1}, \psi_{i-1} \)の式を移項するだけで導出できます.このように,実はテイラー級数と差分近似の式は対応しているんですね. しかも誤差項を見ることによって,近似が何次精度なのか評価もできます.
いきなり"2次精度"とか言われてもまだイメージがつきづらいかもしれません.基本的には次数が増える程,近似計算に使用する点の数がどんどん増えていくようなイメージとなります. テイラー級数をより高次まで採用すると,高次精度の近似式を導出することができます.以下は,微分係数\( \frac{\partial \psi(x_i)}{\partial x} \)の4次精度差分による近似式です.(途中式略)
\[
\frac{\partial \psi(x_i)}{\partial x} = \frac{- \psi_{i+2} + 8 \psi_{i+1} - 8 \psi_{i-1} + \psi_{i-2}}{12h} + O(h^4)
\]
ただし,なんでもかんでも計算精度を上げればいいってもんでもないみたいです.まあ正直,この辺は説明されても実際に自分で計算してみないと実感が沸かないんですよねえ. たくさん失敗して経験を積んでみてください.(投げっぱなし)
次回は,"定常な場合"の方程式を実際に計算していきます.
偏微分方程式の数値計算入門(2/3)