キーワード
密度場から等値面メッシュを生成する
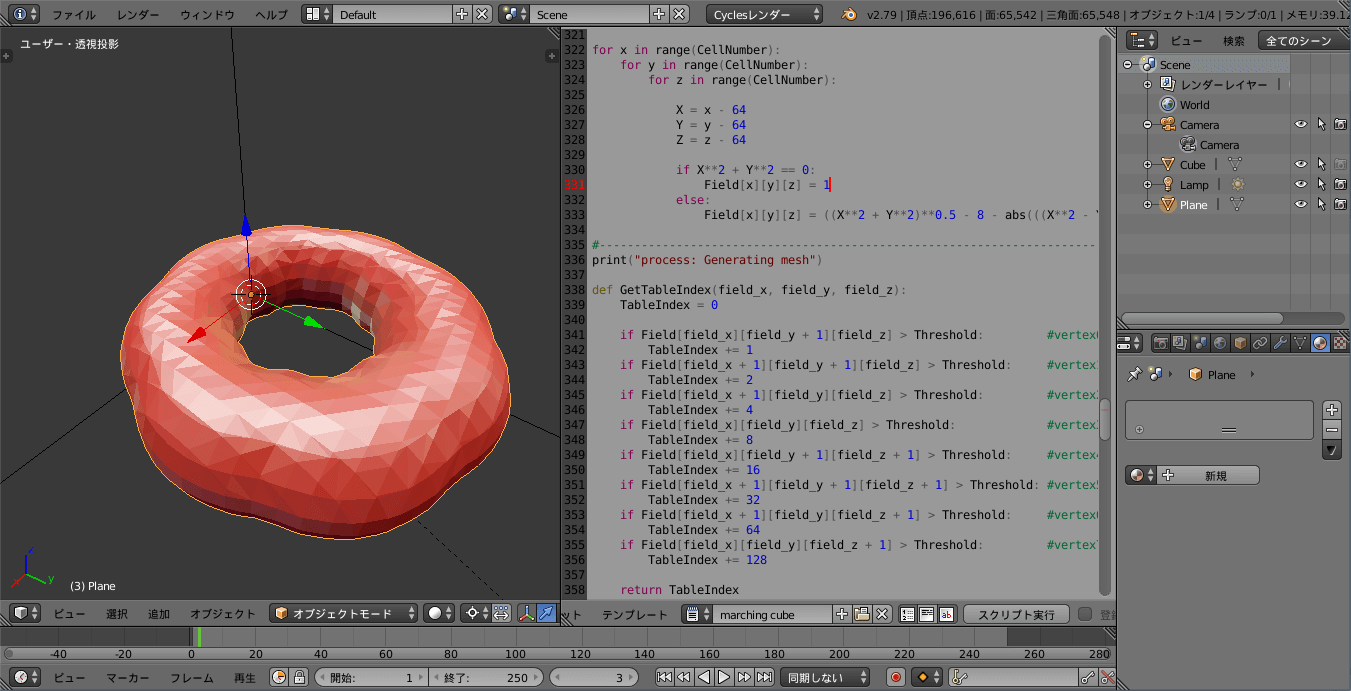
Blenderで3Dグラフを生成する方法についてですが,今回は少しマニアックな内容となります.
天気予報の気圧と等圧線ってありますよね,アレの3次元バージョンだと思ってください.座標(X, Y, Z)に 加えて密度という概念が出てきます.CG用語ではよくボリュームと言われるものです.ただし,今回は ボリュームレンダリングをするのではなく,ボリュームからメッシュに変換する処理をします. この変換にはマーチングキューブ法を用います.詳しくは『マーチングキューブアルゴリズムの解説』で解説しています.
配布ページ
免責事項
- データの使用による損害に対しては当方は一切責任を負わないこととします
スクリプトとしてはまだ中途半端で,全てを自動処理してくれません.それでも触ってみたい好奇心旺盛な方は是非. ついでにいい感じに改良してこちらに戻してくれると嬉しいな(他力本願).
OneDrive
使用方法
- "marching cube.blend"をBlenderで開きます
- テキストエディタを開きます
(画面分割で3Dビューが一緒に見える状態がいいでしょう) - blendファイルに格納されているテキストファイル"marching cube"を開きます
- スクリプト内のField部から密度関数と表示閾値を指定します
密度関数は3次元配列Field[x][y][z]に値を代入することで定義できます. メッシュを生成する閾値はThresholdに値を代入して定義します.定義方法の詳細については 使用例を参照してください.
- スクリプトを実行する前にpythonコンソールを表示しておきます
- スクリプトを実行します
([テキストエディタ]上にマウスカーソルを乗せた状態で[Alt]+[P])
使用例
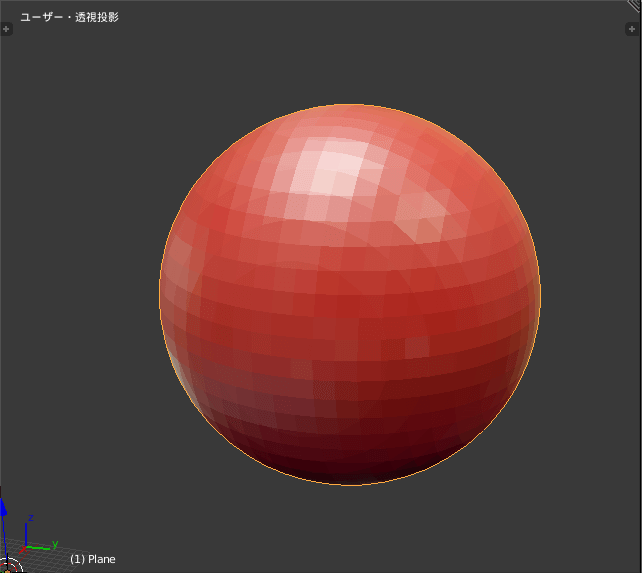
例1:半径10の球体
\[
x^2 + y^2 + z^2 = 10^2
\]
尚,スクリプト内では球体を中心に持ってくるためにx, y, zから分割数の半分,すなわち64を引いた値をX, Y, Zとして扱っています.
#Field------------------------------------------------------------------------------------------
print("process: Generating field")
Threshold = 10**2
for x in range(CellNumber):
for y in range(CellNumber):
for z in range(CellNumber):
X = x - 64
Y = y - 64
Z = z - 64
Field[x][y][z] = X**2 + Y**2 + Z**2
例2:1次平面
\[
x + y + z = 0
\]
#Field------------------------------------------------------------------------------------------
print("process: Generating field")
Threshold = 0
for x in range(CellNumber):
for y in range(CellNumber):
for z in range(CellNumber):
X = x - 64
Y = y - 64
Z = z - 64
Field[x][y][z] = X + Y + Z
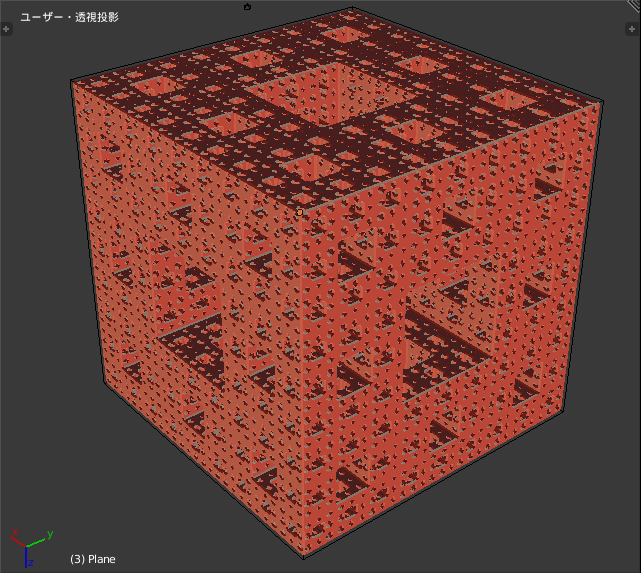
例3:メンガーのスポンジ
式を1本に束ねると恐ろしく煩雑な式になるので段階を踏みながら,下の方から見て行けば何となく流れはわかるかな.\[
F( \vec{x} ) = M(\vec{x}, \vec{\alpha}, \vec{\beta}) = 0.5 \\
M(\vec{x}, \vec{\alpha}, \vec{\beta}) = \displaystyle \prod_{L=1}^\lambda m_D \left( \vec{x}, 3 \left\lfloor 3^{-L} (\vec{\beta} - \vec{\alpha}) + \vec{x} \right\rfloor, 3 \left\lceil 3^{-L} (\vec{\beta} - \vec{\alpha}) + \vec{x} \right\rceil \right) \\
m_D(\vec{x}, \vec{a}, \vec{b}) = \left\lceil \displaystyle \sum_{d=1}^{D} \left( \frac{ \prod_{n=1}^D m_1(x_n, a_n, b_n) }{m_1(x_d, a_d, b_d)} \right) / D \right\rceil \\
m_1(x, a, b) =
\begin{cases}
1 & \left[ a < x \leq a + \frac{1}{3} (b - a) \right] \\
0 & \left[ a + \frac{1}{3} (b - a) < x \leq a + \frac{2}{3} (b - a) \right] \\
1 & \left[ a + \frac{2}{3} (b - a) < x \leq b \right]
\end{cases}
\]
ここで,
\[
D = 3 \Rightarrow \vec{x} = (x_1, x_2, x_3) = (x, y, z) \\
\vec{\alpha} = (1, 1, 1), \vec{\beta} = (128, 128, 128)
\]
λは自己相似の最大反復回数を示しています.λが増える程穴の数が増えます.λが無限になれば出力される図形は消滅します. スクリプトではボクセルサイズより小さな穴が生成されないように制限がかかっています.
#Field------------------------------------------------------------------------------------------
print("process: Generating field")
Threshold = 0.5
def Menger(a, b, x, y, z, level):
def M(a, b, x):
if x >= (a + (b-a) / 3) and x < (a + 2 * (b-a) / 3):
return 0
else:
return 1
def M3D(ax, bx, ay, by, az, bz, xx, yy, zz):
if (M(ay, by, yy) * M(az, bz, zz) == 0) and (M(ax, bx, xx) * M(az, bz, zz) == 0) and (M(ax, bx, xx) * M(ay, by, yy) == 0):
return 0
else:
return 1
def NFloor(n, x):
S = x - x % n
return S
def NCeil(n, x):
S = x + (n - x % n)
return S
V = 1
for L in range(0,level):
holesize = (b-a)*3**-L
if holesize <= CellSize*3.0:
break
ax = NFloor(holesize, x)
bx = NCeil(holesize, x)
ay = NFloor(holesize, y)
by = NCeil(holesize, y)
az = NFloor(holesize, z)
bz = NCeil(holesize, z)
V = V * M3D(ax, bx, ay, by, az, bz, x, y, z)
if x < a or x > b or y < a or y > b or z < a or z > b:
V = 0
return V
for x in range(CellNumber):
for y in range(CellNumber):
for z in range(CellNumber):
Field[x][y][z] = Menger(1, CellNumber, x, y, z, 15)
注意点
前述した通り,本スクリプトは中途半端なもので全自動ではありません.具体的には,このスクリプトはメッシュの生成 を行うものではなく,メッシュの頂点を移動させているだけです.つまり,メッシュは スクリプト実行前にblendファイルに仕込まれており存在しています.配布したファイルでは,スケール0の3角形メッシュが262,144個配置されています.ここで注意が必要なのは スクリプト実行によって可視化されるメッシュ数が262,144個を超えるとエラーを吐くということです. 複雑な図形でメッシュ数がこの個数を超える場合は手動でメッシュを増やす必要があります.
メッシュの生成を自動化しようとすると処理が重くなってしまうんですよねえ,実用レベルのスピードにするには 工夫が必要そうです.